Jolt is a RISC-V zkVM uniquely designed around sumcheck and lookup arguments (Just One Lookup Table).

Jolt is fast (state-of-the-art performance on CPU) and relatively simple (thanks to its lookup-centric architecture).

This book has the following top-level sections:

1. Intro (you are here)
2. Usage (how to use Jolt in your applications)
3. How it works (how the proof system and implementation work under the hood)
4. Roadmap (what's next for Jolt)

Related reading

Papers

Jolt: SNARKs for Virtual Machines via Lookups
Arasu Arun, Srinath Setty, Justin Thaler

Twist and Shout: Faster memory checking arguments via one-hot addressing and increments
Srinath Setty, Justin Thaler

Unlocking the lookup singularity with Lasso
Srinath Setty, Justin Thaler, Riad Wahby

Blog posts

Initial launch:

• Releasing Jolt
• FAQ on Jolt's initial implementation

Updates:

• Nov 12, 2024 blog video
• Aug 18, 2025 (Twist and Shout upgrade) blog

Background

• Proofs, Arguments, and Zero-Knowledge

Credits

Jolt was initially forked from Srinath Setty's work on microsoft/Spartan, specifically the arkworks-rs/Spartan fork in order to use the excellent arkworks-rs field and curve implementations. Jolt uses its own fork of arkworks-algebra with certain optimizations, including some described here. Jolt's R1CS is also proven using a version of Spartan (forked from the microsoft/Spartan2 codebase) optimized for Jolt's uniform R1CS constraints. Jolt uses Dory as its PCS, implemented in spaceandtimefdn/sxt-dory.

Usage

• Quickstart
• Guests and hosts
  • Guests
  • Hosts
• Standard Library
• Profiling
  • zkVM profiling
  • Guest profiling
• Troubleshooting

Quickstart

Installing

Start by installing the jolt command line tool.

cargo +nightly install --git https://github.com/a16z/jolt --force --bins jolt

Creating a Project

To create a project, use the jolt new command.

jolt new <PROJECT_NAME>

This will create a template Jolt project in the specified location. Make sure to cd into the project before running the next step.

cd <PROJECT_NAME>

Project Tour

The main folder contains the host, which is the code that can generate and verify proofs. Within this main folder, there is another package called guest which contains the Rust functions that we can prove from the host. For more information about these concepts refer to the guests and hosts section.

We'll start by taking a look at our guest. We can view the guest code in guest/src/lib.rs.

#![allow(unused)]
#![cfg_attr(feature = "guest", no_std)]
#![no_main]

fn main() {
#[jolt::provable]
fn fib(n: u32) -> u128 {
    let mut a: u128 = 0;
    let mut b: u128 = 1;
    let mut sum: u128;
    for _ in 1..n {
        sum = a + b;
        a = b;
        b = sum;
    }
    b
}
}

As we can see, this implements a simple Fibonacci function called fib. All we need to do to make our function provable is add the jolt::provable macro above it.

Next let's take a look at the host code in src/main.rs.

pub fn main() {
    let (prove_fib, verify_fib) = guest::build_fib();

    let (output, proof) = prove_fib(50);
    let is_valid = verify_fib(proof);

    println!("output: {output}");
    println!("valid: {is_valid}");
}

This section simply imports guest::build_fib which is automatically generated by the jolt::provable macro, and returns functions for proving and verifying our function. The prove function takes the same inputs as the original fib function, but modifies the outputs to additionally return a proof. The verify function can then be used to check this proof, and return a boolean indicating its validity.

Running

Let's now run the host with cargo.

cargo run --release

This will compile the guest, perform some required preprocessing, and execute the host code which proves and verifies the 50th Fibonacci number. This preprocessing is run within the build_fib function and adds significant time to running the host, but only needs to be performed once. This means that we could use the prove method many times without rerunning build_fib. In the future we will support caching this across runs of the host.

Development

Rust

To build Jolt from source, you will need Rust:

• curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh
• Rustup should automatically install the Rust toolchain and necessary targets on the first cargo invocation. You may also need to add the RISC-V target for building guest programs manually: rustup target add riscv32im-unknown-none-elf.

mdBook

To build this book from source:

cargo install mdbook mdbook-katex

For watching the changes in your local browser:

mdbook watch book --open

Guests and Hosts

Guests and hosts are the main concepts that we need to understand in order to use Jolt as an application developer. Guests contain the functions that Jolt will prove, while hosts are where we invoke the prover and verifier for our guest functions.

Guests

Guests contain functions for Jolt to prove. Making a function provable is as easy as ensuring it is inside the guest package and adding the jolt::provable macro above it.

Let's take a look at a simple guest program to better understand it.

#![allow(unused)]
#![cfg_attr(feature = "guest", no_std)]

fn main() {
#[jolt::provable]
fn add(x: u32, y: u32) -> u32 {
    x + y
}
}

As we can see, the guest looks like a normal no_std Rust library. The only major change is the addition of the jolt::provable macro, which lets Jolt know of the function's existence. The only requirement of these functions is that its inputs are serializable and outputs are deserializable with serde. Fortunately serde is prevalent throughout the Rust ecosystem, so most types will support it by default.

There is no requirement that just a single function lives within the guest, and we are free to add as many as we need. Additionally, we can import any no_std compatible library just as we normally would in Rust.

#![allow(unused)]
#![cfg_attr(feature = "guest", no_std)]

fn main() {
use sha2::{Sha256, Digest};
use sha3::{Keccak256, Digest};

#[jolt::provable]
fn sha2(input: &[u8]) -> [u8; 32] {
    let mut hasher = Sha256::new();
    hasher.update(input);
    let result = hasher.finalize();
    Into::<[u8; 32]>::into(result)
}

#[jolt::provable]
fn sha3(input: &[u8]) -> [u8; 32] {
    let mut hasher = Keccak256::new();
    hasher.update(input);
    let result = hasher.finalize();
    Into::<[u8; 32]>::into(result)
}
}

Standard Library

Jolt supports the Rust standard library. To enable support, simply add the guest-std feature to the Jolt import in the guest's Cargo.toml file and remove the #![cfg_attr(feature = "guest", no_std)] directive from the guest code.

Example

#![allow(unused)]
fn main() {
[package]
name = "guest"
version = "0.1.0"
edition = "2021"

[features]
guest = []

[dependencies]
jolt = { package = "jolt-sdk", git = "https://github.com/a16z/jolt", features = ["guest-std"] }
}

#![allow(unused)]

fn main() {
#[jolt::provable]
fn int_to_string(n: i32) -> String {
    n.to_string()
}
}

alloc

Jolt provides an allocator which supports most containers such as Vec and Box. This is useful for Jolt users who would like to write no_std code rather than using Jolt's standard library support. To use these containers, they must be explicitly imported from alloc. The alloc crate is automatically provided by rust and does not need to be added to the Cargo.toml file.

Example

#![allow(unused)]
#![cfg_attr(feature = "guest", no_std)]

fn main() {
extern crate alloc;
use alloc::vec::Vec;

#[jolt::provable]
fn alloc(n: u32) -> u32 {
    let mut v = Vec::<u32>::new();
    for i in 0..100 {
        v.push(i);
    }

    v[n as usize]
}
}

Print statements

Jolt provides utilities emulating print! and println! in a guest program.

Example

#![allow(unused)]
fn main() {
use jolt::{jolt_print, jolt_println};

#[jolt::provable(memory_size = 10240, max_trace_length = 65536)]
fn int_to_string(n: i32) -> String {
    jolt_print!("Hello, ")
    jolt_println!("from int_to_string({n})!");
    n.to_string()
}
}

Note that jolt_print and jolt_println support format strings. The printed strings are written to stdout during RISC-V emulation of the guest.

Hosts

Hosts are where we can invoke the Jolt prover to prove functions defined within the guest.

The host imports the guest package, and will have automatically generated functions to build each of the Jolt functions. For the SHA3 example we looked at in the guest section, the jolt::provable procedural macro generates several functions that can be invoked from the host (shown below):

• compile_sha3(target_dir) to compile the SHA3 guest to RISC-V
• preprocess_prover_sha3 and verifier_preprocessing_from_prover_sha3 to generate the prover and verifier preprocessing. Note that the preprocessing only needs to be generated once for a given guest program, and can subsequently be reused to prove multiple invocations of the guest.
• build_prover_sha3 returns a closure for the prover, which takes in the same input types as the original function and modifies the output to additionally include a proof.
• build_verifier_sha3 returns a closure for the verifier, which verifies the proof. The verifier closure's parameters comprise of the program input, the claimed output, a bool value claiming whether the guest panicked, and the proof.

pub fn main() {
    let target_dir = "/tmp/jolt-guest-targets";
    let mut program = guest::compile_sha3(target_dir);

    let prover_preprocessing = guest::preprocess_prover_sha3(&mut program);
    let verifier_preprocessing =
        guest::verifier_preprocessing_from_prover_sha3(&prover_preprocessing);

    let prove_sha3 = guest::build_prover_sha3(program, prover_preprocessing);
    let verify_sha3 = guest::build_verifier_sha3(verifier_preprocessing);

    let input: &[u8] = &[5u8; 32];
    let now = Instant::now();
    let (output, proof, program_io) = prove_sha3(input);
    println!("Prover runtime: {} s", now.elapsed().as_secs_f64());
    let is_valid = verify_sha3(input, output, program_io.panic, proof);

    println!("output: {}", hex::encode(output));
    println!("valid: {is_valid}");
}

Profiling

If you're an application developer, you may want to profile your guest program: fewer cycles = faster proof. If so, check out Guest profiling.

If you're contributing to Jolt, you may be interested in profiling Jolt itself, in which case you should check out zkVM profiling

Profiling Jolt

Execution profiling

Jolt is instrumented using tokio-rs/tracing for execution profiling. We use the tracing_chrome crate to output traces in the format expected by Perfetto.

To generate a trace, run e.g.

cargo run --release -p jolt-core profile --name sha3 --format chrome

Where --name can be sha2, sha3, sha2-chain, fibonacci, or btreemap. The corresponding guest programs can be found in the examples directory. The benchmark inputs are provided in bench.rs.

The above command will output a JSON file in the workspace rootwith a name trace-<timestamp>.json, which can be viewed in Perfetto:

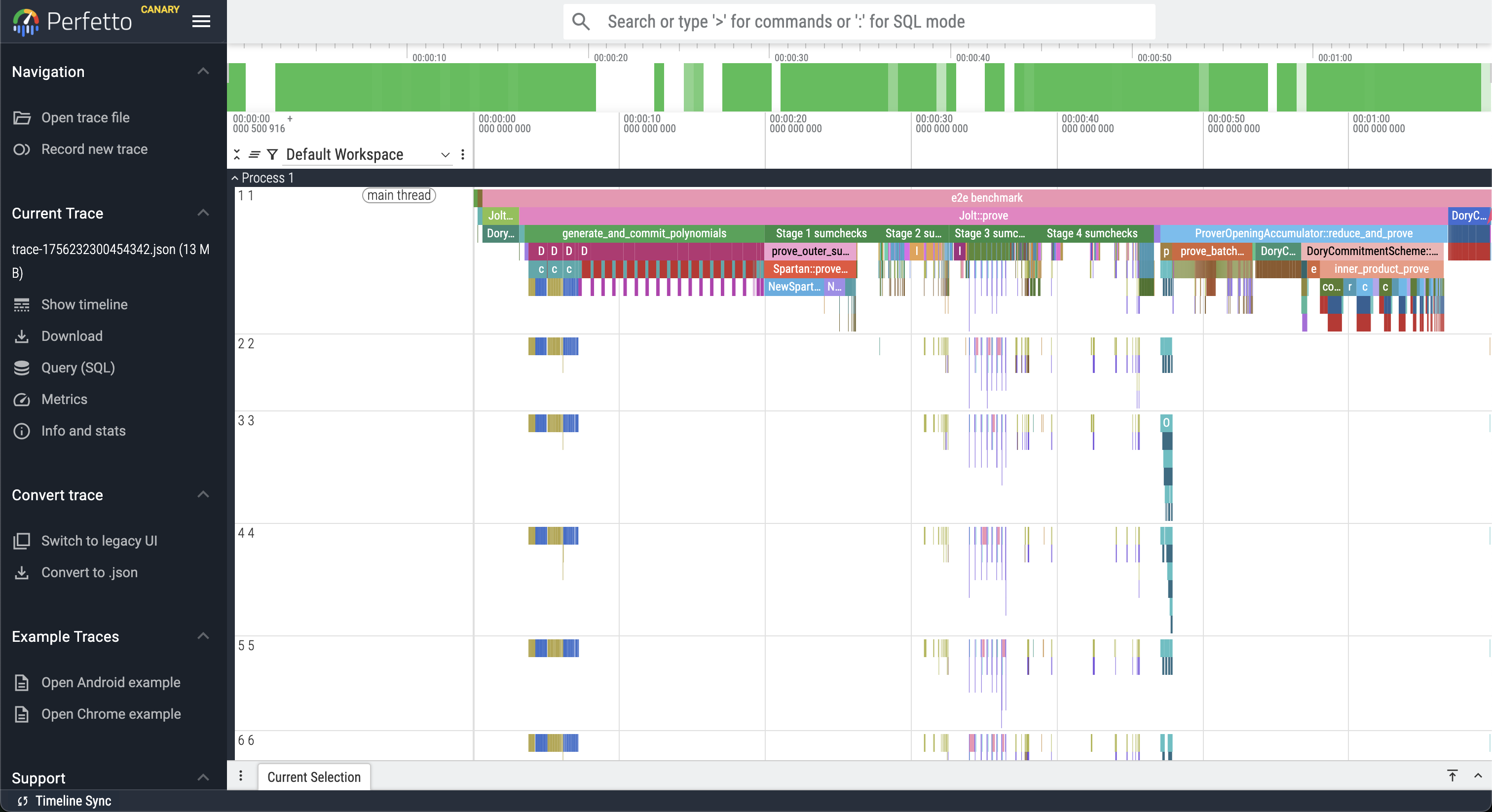
Memory profiling

Jolt uses allocative for memory profiling. Allocative allows you to (recursively) measure the total heap space occupied by any data structure implementing the Allocative trait, and optionally generate a flamegraph. In Jolt, most sumcheck data structures implement the Allocative trait, and we generate a flamegraph at the start and end of stages 2-5 of the Jolt DAG (see jolt_dag.rs).

To generate allocative output, run:

RUST_LOG=debug cargo run --release --features allocative -p jolt-core profile --name sha3 --format chrome

Where, as above, --name can be sha2, sha3, sha2-chain, fibonacci, or btreemap.

The above command will log memory usage info to the command line and output multiple SVG files, e.g. stage3_start_flamechart.svg, which can be viewed in a web browser of your choosing:

Guest Profiling

This section details the available tools to profile guest programs. There is currently a single utility available: Cycle-Tracking, which is detailed below.

Cycle-Tracking in Jolt

Measure real (RV32IM) and virtual cycles inside your RISC-V guest code with zero-overhead markers. This is useful when analyzing the mapping between the high-level guest program and the equivalent compiled program to be proven by Jolt.

Note: The Rust compiler will often shuffle around your implementation for optimization purposes, which can affect cycle tracking. If you suspect the compiler is interfering with profiling, then use the Hint module. For example, wrap values in core::hint::black_box() (see below) to help keep your measurements honest.

API

Under the hood each marker emits an ECALL signaling the emulator to track your code segment.

Example

#![allow(unused)]
#![cfg_attr(feature = "guest", no_std)]
fn main() {
use jolt::{start_cycle_tracking, end_cycle_tracking};

#[jolt::provable]
fn fib(n: u32) -> u128 {
    let (mut a, mut b) = (0, 1);

    start_cycle_tracking("fib_loop");
    for _ in 1..n {
        let sum = a + b;
        a = b;
        b = sum;
    }
    end_cycle_tracking("fib_loop");

    b
}
}

Hinting the compiler

#![allow(unused)]
#![cfg_attr(feature = "guest", no_std)]
fn main() {
use core::hint::black_box;

#[jolt::provable]
fn muldiv(a: u32, b: u32, c: u32) -> u32 {
    use jolt::{end_cycle_tracking, start_cycle_tracking};

   start_cycle_tracking("muldiv");
   let result = black_box(a * b / c); // use black_box to keep code in place
   end_cycle_tracking("muldiv");

   result
}
}

Wrap inputs or outputs that must stay observable during the span. In the above example, a * b / c gets moved to the return line without black_box(), causing inaccurate measurements. To run the above example, use cargo run --release -p muldiv.

Expected Output

"muldiv": 9 RV32IM cycles, 16 virtual cycles
Trace length: 533
Prover runtime: 0.487551667 s
output: 2223173
valid: true

Troubleshooting

Insufficient Memory or Stack Size

Jolt provides reasonable defaults for the total allocated memory and stack size. It is however possible that the defaults are not sufficient, leading to unpredictable errors within our tracer. To fix this we can try to increase these sizes. We suggest starting with the stack size first as this is much more likely to run out.

Below is an example of manually specifying both the total memory and stack size.

#![allow(unused)]
#![cfg_attr(feature = "guest", no_std)]
#![no_main]

fn main() {
extern crate alloc;
use alloc::vec::Vec;

#[jolt::provable(stack_size = 10000, memory_size = 10000000)]
fn waste_memory(size: u32, n: u32) {
    let mut v = Vec::new();
    for i in 0..size {
        v.push(i);
    }
}
}

Maximum Input or Output Size Exceeded

Jolt restricts the size of the inputs and outputs to 4096 bytes by default. Using inputs and outputs that exceed this size will lead to errors. These values can be configured via the macro.

#![allow(unused)]
#![cfg_attr(feature = "guest", no_std)]
#![no_main]

fn main() {
#[jolt::provable(max_input_size = 10000, max_output_size = 10000)]
fn sum(input: &[u8]) -> u32 {
    let mut sum = 0;
    for value in input {
        sum += *value as u32;
    }

    sum
}
}

Guest Attempts to Compile Standard Library

Sometimes after installing the toolchain the guest still tries to compile with the standard library which will fail with a large number of errors that certain items such as Result are referenced and not available. This generally happens when one tries to run jolt before installing the toolchain. To address, try rerunning jolt install-toolchain, restarting your terminal, and delete both your rust target directory and any files under /tmp that begin with jolt.

Guest Fails to Compile on the Host

By default, Jolt will attempt to compile the guest for the host architecture. This is useful if you want to run and test the guest's tagged functions directly. If you know your guest code cannot compile on the host (for example, if your guest uses inline RISCV assembly), you can specify to only build for the guest architecture.

#![allow(unused)]
fn main() {
#[jolt::provable(guest_only)]
fn inline_asm() -> (i32, u32, i32, u32) {
    use core::arch::asm;

    let mut data: [u8; 8] = [0; 8];
    unsafe {
        let ptr = data.as_mut_ptr();

        // Store Byte (SB instruction)
        asm!(
        "sb {value}, 0({ptr})",
        ptr = in(reg) ptr,
        value = in(reg) 0x12,
        );
    }
}
}

Getting Help

If none of the above solve the problem, please create a Github issue with a detailed bug report including the Jolt commit hash, the hardware or container configuration used, and a minimal guest program to reproduce the bug.

How it works

This section dives into in the inner workings of Jolt, beyond what an application developer needs to know. It covers the architecture, design decisions, and implementation details of Jolt. Proceed if you:

• have been poking around the Jolt codebase and have questions about why something is implemented the way it is

• have read some papers (Jolt, Twist/Shout) and want to know how things fit together in practice

• would like to start contributing to Jolt

This section is comprised of the following subsections:

• Architecture overview
  • RISC-V emulation
  • R1CS constraints
  • Registers
  • RAM
  • Instruction execution
  • Bytecode
  • Batched opening proof
• Twist and Shout
• Dory
• Optimizations
  • Batched sumcheck
  • Batched openings
  • Inlines
  • Leveraging uniformity in Spartan
  • Small value optimizations
  • EQ optimizations
• Appendix
  • Terminology and nomenclature
  • Multilinear extensions
  • Sumcheck
  • Polynomial commitment schemes
  • Memory checking and lookup arguments
  • RISC-V
  • Jolt 0.1.0
  • Additional resources

Architecture overview

This section gives a overview of the architecture of the Jolt codebase.

The following diagram depicts the end-to-end Jolt pipeline, which is typical of RISC-V zkVMs.

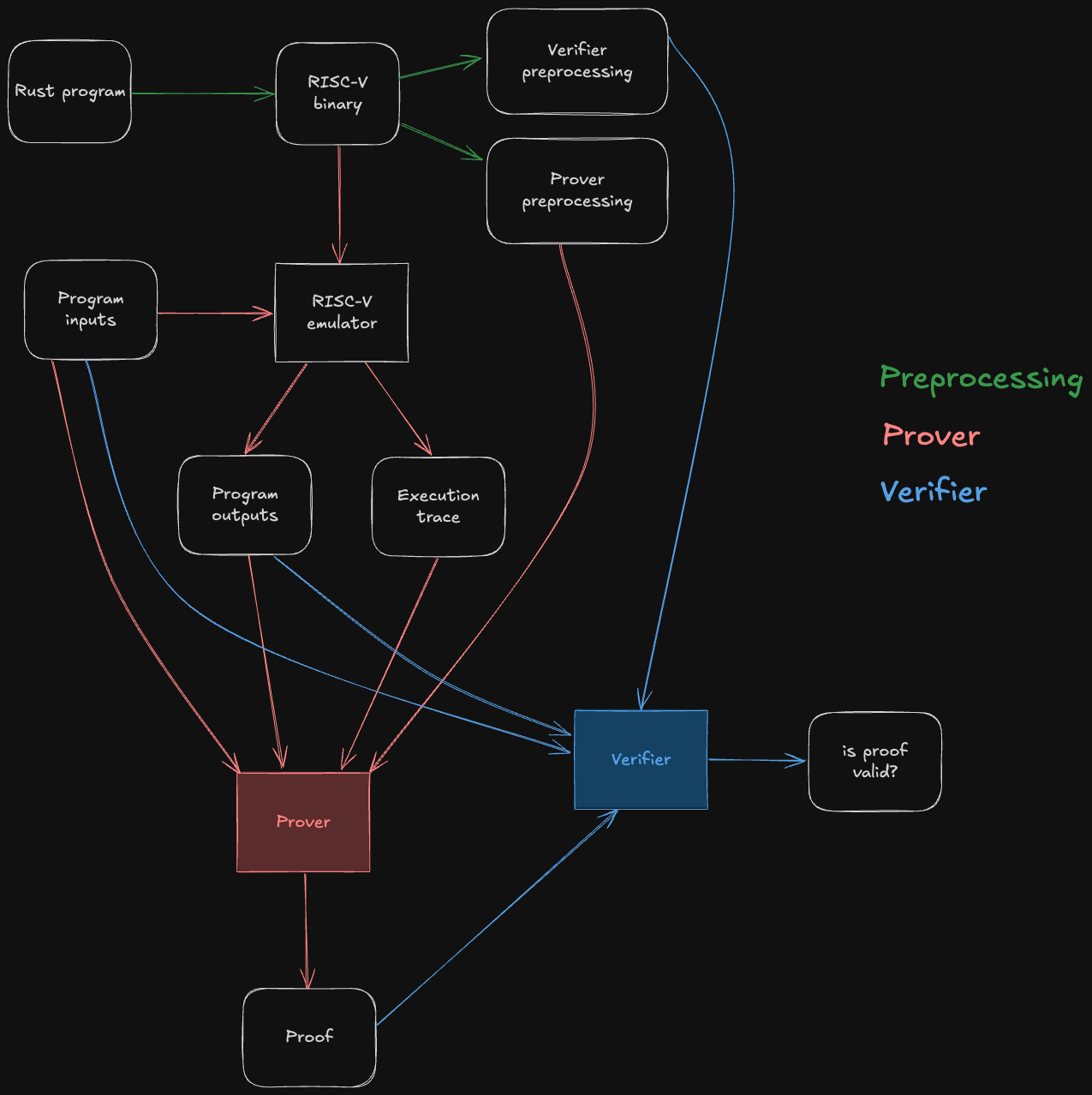
The green steps correspond to preprocessing steps, which can be computed ahead of time from the guest program's bytecode. Note that they do not depend on the program inputs, so the preprocessing data can be reused across multiple invocations of the Jolt prover/verifier.

The red steps correspond to the prover's workflow: it runs the guest program on some inputs inside of a RISC-V emulator, producing the output of the program as well as an execution trace. This execution trace, along with the inputs, outputs, and preprocessing, are then passed to the Jolt prover, which uses them to generate a succinct proof that the outputs are the result of correctly executing the given guest program on the inputs.

The blue steps correspond to the verifier's workflow. The verifier does not emulate the guest program, not does it receive the execution trace (which may be billions of cycles long) from the prover. Instead, it receives the proof from the prover, and uses it to check that the guest program produces claimed outputs when run on the given inputs.

For the sake of readability, the diagram above abstracts away all of Jolt's proof system machinery. The rest of this section aims to disassemble the underlying machinery in useful-but-not-overwhelming detail.

As a starting point, we will present two useful mental models of the Jolt proof system: Jolt as a CPU, and Jolt as a DAG (a different DAG than the one above; we love DAGs).

Jolt as a CPU

One way to understand Jolt is to map the components of the proof system to the components of the virtual machine (VM) whose functionality they prove.

Jolt's five components

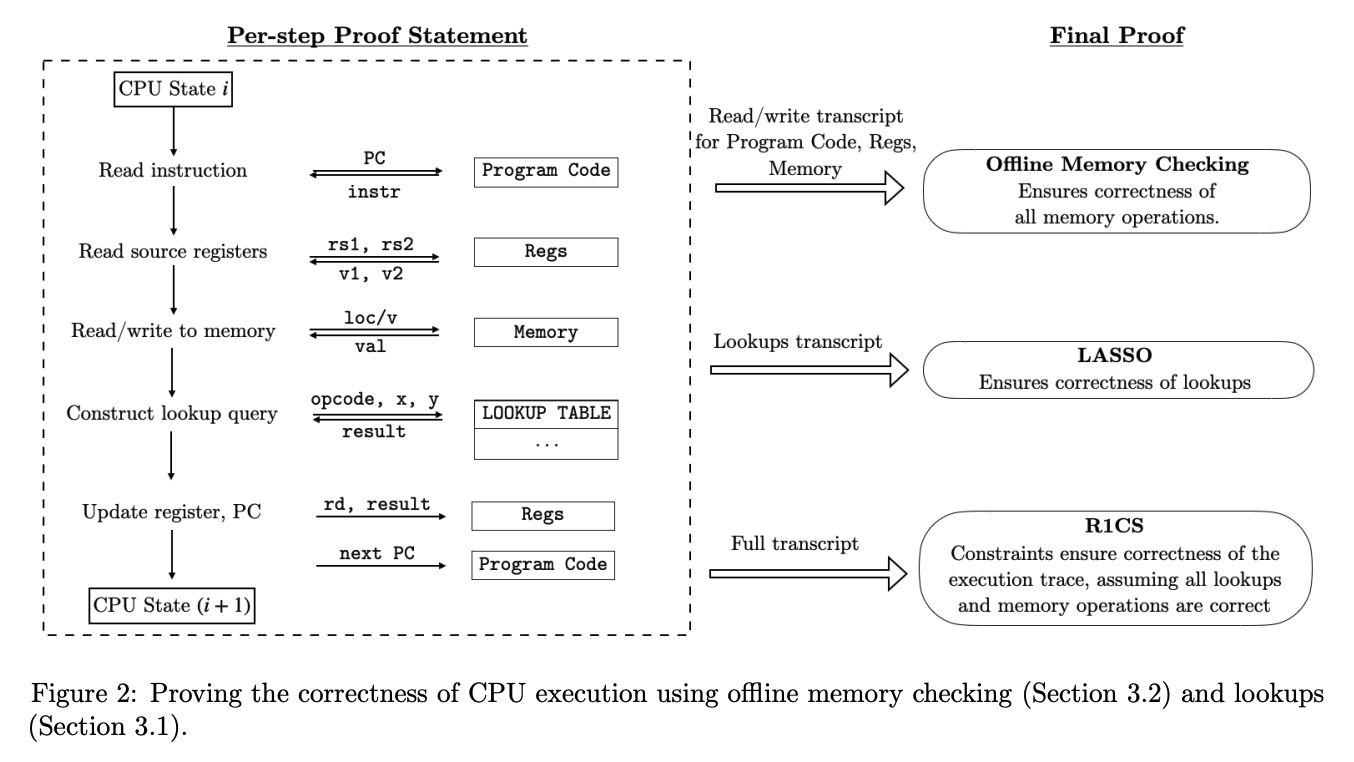
A VM does two things:

• Repeatedly execute the fetch-decode-execute logic of its instruction set architecture.
• Perform reads and writes to memory.

The Jolt paper depicts these two tasks mapped to three components in the Jolt proof system:

The Jolt codebase is similarly organized, but instead distinguishes read-write memory (comprising registers and RAM) from program code (aka bytecode, which is read-only), for a total of five components:

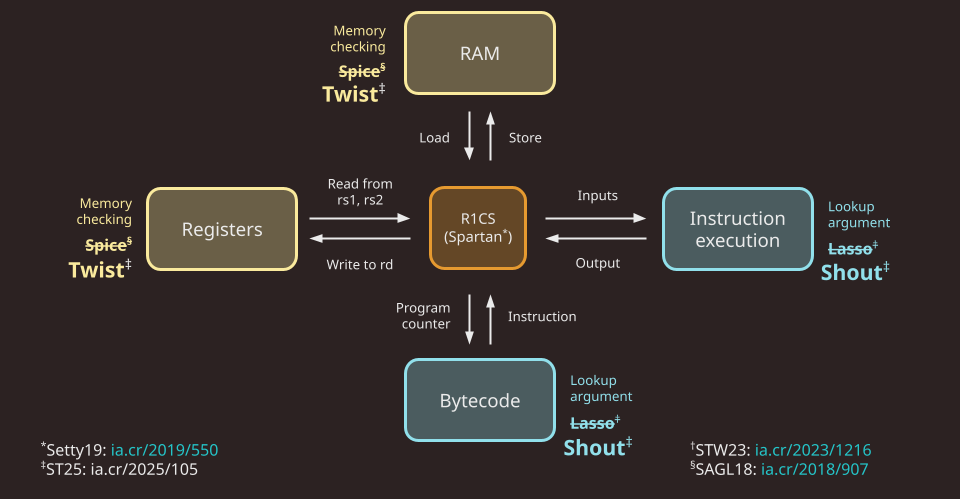
Note that in Jolt as described in the paper, as well as in the first version of the Jolt implementation (v0.1.0), the memory checking and lookup argument used are Spice and Lasso, respectively. As of v0.2.0, Jolt replaces Spice and Lasso with Twist and Shout, respectively.

R1CS constraints

To handle the "fetch" part of the fetch-decode-execute loop, there is a minimal R1CS instance (about 30 constraints per cycle of the RISC-V VM). These constraints handle program counter (PC) updates and serves as the "glue" enforcing consistency between polynomials used in the components below. Jolt uses Spartan, optimized for the highly-structured nature of the constraint system (i.e. the same small set of constraints are applied to every cycle in the execution trace).

For more details: R1CS constraints

RAM

To handle reads/writes to RAM Jolt uses the Twist memory checking argument.

For more details: RAM

Registers

Similar to RAM, Jolt uses the Twist memory checking argument to handle reads/writes to registers.

For more details: Registers

Instruction execution

To handle the "execute" part of the fetch-decode-execute loop, Jolt invokes the Shout lookup argument. The lookup table, in this case, effectively maps every instruction to its correct output.

For more details: Instruction execution

Bytecode

To handle the "decode" part of the fetch-decode-execute loop, Jolt uses another instance of Shout. The bytecode of the guest program is "decoded" in preprocessing, and the prover subsequently invokes offline memory-checking on the sequence of reads from this decoded bytecode corresponding to the execution trace being proven.

For more details: Bytecode

Jolt as a DAG

One useful way to understand Jolt is to view it as a directed acyclic graph (DAG). That might sound surprising -- how can a zkVM be represented as a DAG? The key lies in the structure of its sumchecks, and in particular, the role of virtual polynomials.

Virtual vs. Committed Polynomials

Virtual polynomials, introduced in the Binius paper, are used heavily in Jolt.

A virtual polynomial is a part of the witness that is never committed directly. Instead, any claimed evaluation of a virtual polynomial is proven by a subsequent sumcheck. In contrast, committed polynomials are committed to explicitly and their evaluaions are proven using the opening proof of the PCS.

Sumchecks as Nodes

Each sumcheck in Jolt corresponds to a node in the DAG. Consider the following hypothetical sumcheck expression:

$$\text{InputClaim}\stackrel{?}{=}\sum _{x\in \{0,1{\}}^n}f(x)\cdot g(x)+h(x)$$

Here, the left-hand side is the input claim, and the right-hand side is a sum over the Boolean hypercube of a multivariate polynomial of degree 2, involving three multilinear terms $f$, $g$, and $h$. The sumcheck protocol reduces this input claim to three output claims about $f$, $g$, and $h$:

$$\begin{gathered} {\text{OutputClaim}}_f\stackrel{?}{=}f(r) \\ {\text{OutputClaim}}_g\stackrel{?}{=}g(r) \\ {\text{OutputClaim}}_h\stackrel{?}{=}h(r) \end{gathered}$$

where $r\in {\mathbb{F}}^n$ consists of the random challenges obtained over the course of the sumcheck.

An output claim of one sumcheck might be the input claim of another sumcheck. Recall that by definition, the output claim for a virtual polynomial is necessarily the input claim of another sumcheck.

It follows that input claims can be viewed as in-edges and output claims as out-edges, thus defining the graph structure. This is what the Jolt sumcheck dag looks like:

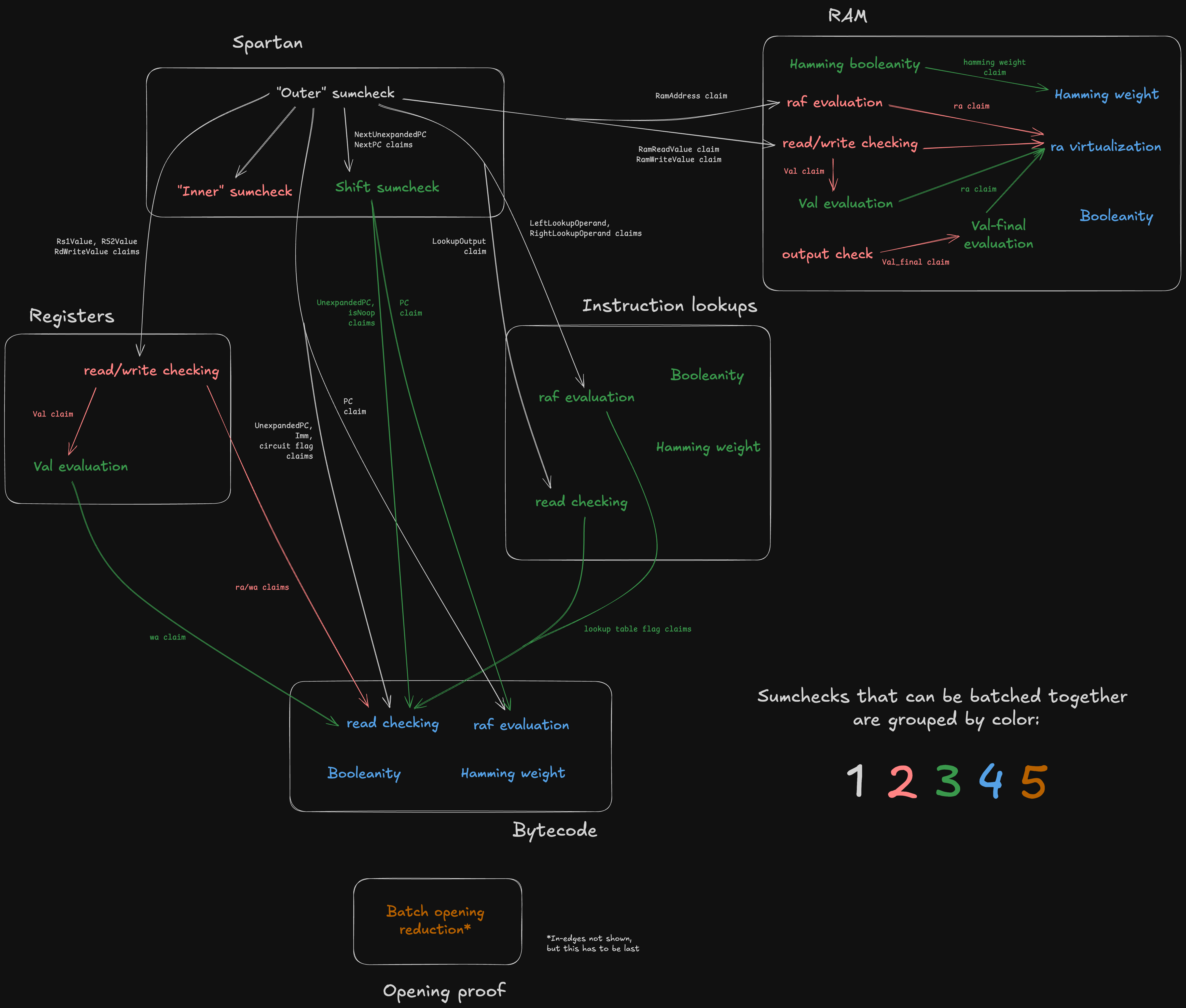
Note the white boxes corresponding to the five components of Jolt under the CPU paradigm –– plus an extra component for the opening proof, which doesn't have a CPU analogue.

In the diagaram above, sumchecks are color-coded based on "batch"; sumchecks in the same batch are "run in parallel" (see Batched sumcheck). Note that a given component may include sumchecks in different batches. For example, the three sumchecks in Spartan span stages 1, 2, and 3.

This is codified by the SumcheckStages trait, which defines methods stage1_prove, stage1_verify, stage2_prove, stage2_verify, etc. Each component implements SumcheckStages, declaring each sumcheck in its subgraph and which stage it belongs to. Observe that the DAG defines a partial ordering over the nodes (sumchecks), which consequently defines the minimum number of batches -- two sumchecks cannot be batched together if one "depends" on the other.

The batched opening proof subprotocol involves a batched sumcheck which is necessarily last (i.e. stage 5), because its input claims are obtained from all the committed polynomial evaluations from the previous stages. For more details on the batched opening proof subprotocol, see Opening proof.

Managing state and data flow

The StateManager is responsible for tracking and managing the state persisted across all the sumcheck stages in Jolt. In particular, it contains an Openings map to manage the flow of claimed evaluations –– the edges of the DAG. It's a mapping from an OpeningId to a claimed polynomial evaluation. As sumchecks are proven, their output claims (for both virtual and committed polynomials) are inserted into the map. Later sumchecks can then consume the virtual polynomial openings as input claims.

While virtual polynomial claims are used internally and passed between sumchecks, committed polynomial claims are tracked because they must ultimately be verified via a batched Dory opening proof at the end of the protocol.

RISC-V emulation

Jolt's RISC-V emulator is implemented within the tracer crate. It originated as a fork of the riscv-rust project and has since evolved significantly to support Jolt’s unique requirements. The bulk of the emulator's logic resides in the instruction subdirectory of the tracer crate, which defines the behavior of individual RISC-V instructions.

Core traits

Two key traits form the backbone of the RISC-V emulator:

• RISCVInstruction

  • Defines core instruction behavior required by the tracer.
  • Includes two associated constants, MASK and MATCH, used for decoding instructions from raw bytes.
  • Has an associated type Format, indicating the RISC-V instruction format (e.g., R-type or I-type).
  • The associated type RAMAccess specifies memory access (read/write) required by the instruction, guiding the tracer in capturing memory state before and after execution.
  • Its critical method, execute, emulates instruction execution by modifying CPU state and populating memory state changes as needed.

• RISCVTrace (extends RISCVInstruction)

  • Adds a trace method, which by default invokes execute and additionally captures pre- and post-execution states of any accessed registers or memory. May be overridden for instructions which employ virtual sequences, see below.
  • Constructs a RISCVCycle struct instance from the captured information and appends it to a trace vector.

Core enums

RV32IMInstruction and RV32IMCycle are enums encapsulating all RV32IM instruction variants, wrapping implementations of RISCVInstruction and RISCVCycle, respectively.

Virtual Instructions and Sequences

A crucial concept in Jolt is that of virtual instructions and virtual sequences, introduced in section 6 of the Jolt paper. Virtual instructions don't exist in the official RISC-V ISA but are specifically created to facilitate proving.

Reasons for Using Virtual Instructions:

Complex operations (e.g. division)

Some instructions, like division, don't neatly adhere to the lookup table structure required by prefix-suffix Shout. To handle these cases, the problematic instruction is expanded into a virtual sequence, a series of instructions (some potentially virtual).

For instance, division involves a sequence described in detail in section 6.3 of the Jolt paper, utilizing virtual untrusted "advice" instructions. In the context of division, the advice instructions store the quotient and remainder in virtual registers, which are additional registers used exclusively within virtual sequences as scratch space. The rest of the division sequence verifies the correctness of the computed quotient and remainder, finally storing the quotient in the destination register specified by the original instruction.

Performance optimization (inlines)

Virtual sequences can also be employed to optimize prover performance on specific operations, e.g. hash functions. For details, refer to Inlines.

Implementation details

Virtual instructions reside alongside regular instructions within the instructions subdirectory of the tracer crate. Instructions employing virtual sequences implement the VirtualInstructionSequence trait, explicitly defining the sequence for emulation purposes. The execute method executes the instruction as a single operation, while the trace method executes each instruction in the virtual sequence.

Performance considerations

A first-order approximation of Jolt's prover cost profile is "pay-per-cycle": each cycle in the trace costs roughly the same to prove, regardless of which instruction is being proven or whether the given cycle is part of a virtual sequence. This means that instructions that must be expanded to virtual sequences are more expensive than their unexpanded counterparts. An instruction emulated by an eight-instruction virtual sequence is approximately eight times more expensive to prove than a single, standard instruction.

On the other hand, virtual sequences can be used to improve prover performance on key operations (e.g. hash functions). This is discussed in the Inlines section.

R1CS constraints

Jolt employs Rank-1 Constraint System (R1CS) constraints to enforce the state transition function of its RISC-V virtual machine and to serve as a bridge between its various components. Jolt uses Spartan to prove its R1CS constraints.

Enforcing state transition

The R1CS constraints defined in constraints.rs include conditions ensuring that the program counter (PC) is updated correctly for each execution step. These constraints capture:

• The "normal" case, where the PC is incremented to point to the next instruction in the bytecode

• Jump and branch instructions, where the PC may be updated according to some condition and offset

Linking sumcheck instances

Jolt leverages Twist and Shout instances, each comprising sumchecks. Jolt's R1CS constraints provide essential "links" between these sumchecks, enforcing relationships between different polynomials. For example, R1CS ensures consistency between independent components such as the RAM and register Twist instances: for instructions like LB or LW, an R1CS constraint ensures the value read from RAM matches the value written into the destination register (rd). This is critical because RAM and registers operate as independent Twist memory checking instances, and we need to enforce this relationship between otherwise disjoint witnesses.

Arithmetic instructions

While Jolt's design uniquely leverages lookups for most RISC-V instructions, arithmetic instructions are the exception to this rule. Most arithmetic instructions (addition, subtraction, multiplication) are primarily constrained using R1CS constraints, with the lookup only serving to truncate potential overflow bits.

For these instructions, we can emulate the 32-bit arithmetic using native field arithmetic, since Jolt's elliptic curve scalar field is big enough to perform these operations without overflow. E.g. to add two 32-bit numbers x and y, we can add their ${\mathbb{F}}_r$ equivalents $x$ and $y$, knowing that $x+y\in {\mathbb{F}}_r$ will be equivalent to the desired 33-bit sum. We then employ a range-check lookup to truncate the potential overflow bit, thus matching the behavior of the RISC-V spec.

Circuit Flags

Circuit flags, also referred to as operation (op) flags, are boolean indicators associated with each instruction. These circuit flags are deterministically derived from the instruction's opcode and operands as they appear in the bytecode. For this reason, they are treated as "read values" (rv) in the context of the bytecode Shout instance.

Some examples of circuit flags:

• Jump Flag: Indicates jump instructions (JAL, JALR).

• Branch Flag: Indicates branch instructions (e.g. BEQ, BNE).

• Load Flag: Indicates load instructions (e.g. LB, LW).

• Noop Flag: Indicates virtual no-op instructions, used to pad execution traces to a power-of-two length.

These flags appear in the R1CS constraints. For example, the "load" flag enables the aforementioned RAM-to-register constraint specifically for load instructions.

Spartan

🚧 These docs are under construction 🚧

👷If you are urgently interested in this specific page, open a Github issue and we'll try to expedite it.👷

Registers

Jolt proves the correctness of register updates using the Twist memory checking algorithm, specifically utilizing the "local" prover algorithm.

In this Twist instance, $K=64$ because we have 32 RISC-V registers and 32 virtual registers. This is small enough that we can use $d=1$.

Deviations from the Twist algorithm as described in the paper

Our implementation of the Twist prover algorithm differs from the description given in the Twist and Shout paper in a couple of ways. One such deviation is wv virtualization. Other, register-specific deviations are described below.

Two reads, one write per cycle

The Twist algorithm as described in the paper assumes one read and one write per cycle, with corresponding polynomials $\widetilde{\text{ra}}$ (read address) and $\widetilde{\text{wa}}$ (write address). However, in the context of the RV32IM instruction set, a single instruction (specifically, an R-type instruction) can read from two source registers (rs1 and rs2) and write to a destination register (rd).

Thus, we have two $\widetilde{\text{ra}}$ polynomials corresponding to rs1 and rs2, plus a $\widetilde{\text{wa}}$) polynomial corresponding to rd. Similarly, there are two $\widetilde{\text{rv}}$ polynomials and one $\widetilde{\text{wv}}$ polynomial.

As a result, we have two read-checking sumcheck instances and one write-checking sumcheck instance. In practice, all three are batched into a single sumcheck instance.

Why we don't need one-hot checks

Normally in Twist and Shout, polynomials like $\widetilde{\text{ra}}$ and $\widetilde{\text{wa}}$ need to be checked for one-hotness using the Booleanity and Hamming weight sumchecks.

In the context of registers, we do not need to perform these one-hot checks for ${\widetilde{\text{ra}}}_{\text{rs1}}$, ${\widetilde{\text{ra}}}_{\text{rs2}}$, and ${\widetilde{\text{wa}}}_{\text{rd}}$.

Observe that the registers are hardcoded in the program bytecode. Thus we can virtualize ${\widetilde{\text{ra}}}_{\text{rs1}}$, ${\widetilde{\text{ra}}}_{\text{rs2}}$, and ${\widetilde{\text{wa}}}_{\text{rd}}$ using the bytecode read-checking sumcheck. Since the bytecode is known by the verifier and assumed to be "well-formed", the soundness of the read-checking sumcheck effectively ensures the one-hotness of ${\widetilde{\text{ra}}}_{\text{rs1}}$, ${\widetilde{\text{ra}}}_{\text{rs2}}$, and ${\widetilde{\text{wa}}}_{\text{rd}}$.

A (simplified) sumcheck expression to illustrate how this virtualization works:

$${\widetilde{\text{ra}}}_{\text{rs1}}(r_{\text{register}},r_{\text{cycle}})=\sum _{k=(k_1,\dots ,k_d)\in {\left(\{0,1{\}}^{\log (K)/d}\right)}^d,j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r_{\text{cycle}},j)\cdot \left(\prod _{i=1}^d{\widetilde{\text{ra}}}_i(k_i,j)\right)\cdot \widetilde{\text{rd}}(k,r_{\text{register}})$$

where $\widetilde{\text{rd}}(k_{\text{bytecode}},k_{\text{register}})=1$ if the instruction at index $k_{\text{bytecode}}$ in the bytecode has $\text{rs1}=k_{\text{register}}$.

RAM

Jolt proves the correctness of RAM operations using the Twist memory checking algorithm, specifically utilizing the "local" prover algorithm.

Dynamic parameters

In Twist, the parameter $K$ determines the size of the memory. For RAM, unlike registers, $K$ is not known a priori and depends on the memory usage of the guest program. Consequently, the parameter $d$, dictating how the memory address space is partitioned into chunks, must also be dynamically tuned. This ensures that no committed polynomial exceeds a maximum size defined by $T\times K^{1/d}$.

Jolt is currently configured so that $K^{1/d}=2^8$.

Address remapping

We treat each 4-byte-aligned word in the guest memory as one "cell" for the purposes of memory checking. Our RISC-V emulator is configured to use 0x80000000 as the DRAM start address -- the stack and heap occupy addresses above the start address, while Jolt reserves some memory below the start address for program inputs and outputs.

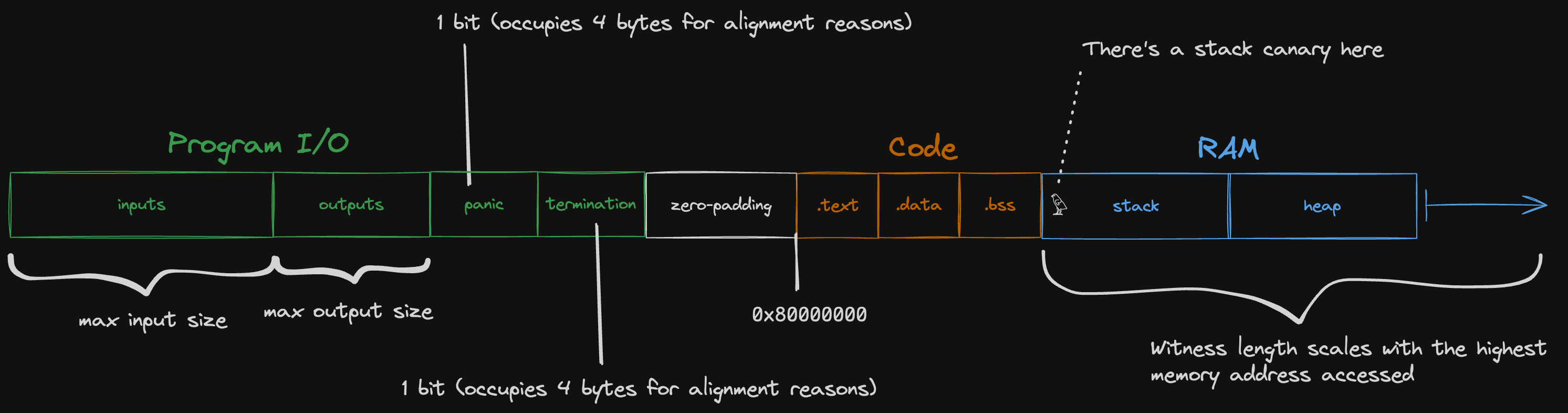
For the purposes of the memory checking argument, we remap the memory address to a witness index:

#![allow(unused)]
fn main() {
(address - memory_layout.input_start) / 4 + 1
}

where input_start is the left-most address depicted in the diagram above. The division by four reflects the fact that we treat guest memory as "word-addressable" for the purposes of memory-checking. Any load or store instructions that access less than a full word (e.g. LB, SH) are expanded into virtual sequences that use the LW or SW instead.

Deviations from the Twist algorithm as described in the paper

Our implementation of the Twist prover algorithm differs from the description given in the Twist and Shout paper in a couple of ways. One such deviation is wv virtualization. Other, RAM-specific deviations are described below.

Single operation per cycle

The Twist algorithm as described in the paper assumes one read and one write per cycle, with corresponding polynomials $\widetilde{\text{ra}}$ (read address) and $\widetilde{\text{wa}}$ (write address). However, in the context of the RV32IM instruction set, only a single memory operation -- either a read or a write (or neither) -- is performed per cycle. Thus, a single polynomial (merging $\widetilde{\text{ra}}$ and $\widetilde{\text{wa}}$) suffices, simplifying and optimizing the algorithm. This polynomial is referred to as $\widetilde{\text{ra}}$ for the rest of this document.

No-op cycles

Many instructions do not access memory, so we represent them using a row of zeros in the $\widetilde{\text{ra}}$ polynomial rather than the one-hot encoding of the accessed address. Having more zeros in $\widetilde{\text{ra}}$ makes it cheaper to commit to and speeds up some of the other Twist sumchecks. This modification necessitates adjustments to the Hamming weight sumcheck, which would otherwise enforce that the Hamming weight for each "row" in $\widetilde{\text{ra}}$ is 1.

We introduce an additional Hamming Booleanity sumcheck:

$$0=\sum _{j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r^{\prime },j)\cdot \left(\widetilde{\text{hw}}(j{)}^2-\widetilde{\text{hw}}(j)\right)$$

where $\widetilde{\text{hw}}$ is the Hamming weight polynomial, which can be virtualized using the original Hamming weight sumcheck expression:

$$\widetilde{\text{hw}}(r_{\text{cycle}})=\sum _{k=(k_1,\dots ,k_d)\in {\left(\{0,1{\}}^{\log (K)/d}\right)}^d}\widetilde{\text{ra}}(k,r_{\text{cycle}})$$

For simplicity, these equations are presented for the $d=1$ case, but as described above, $d$ for RAM is dynamic and can be greater than one.

ra virtualization

In Twist as described in the paper, a higher $d$ parameter would translate to higher sumcheck degree for the read checking, write checking, and $\widetilde{\text{raf}}$ evaluation sumchecks. Moreover, $d>1$ is fundamentally incompatible with the local prover algorithm for the read/write checking sumchecks.

To leverage the local algorithm while still supporting $d>1$, Jolt simply carries out the read checking, write checking, and $\widetilde{\text{raf}}$ evaluation sumchecks as if $d=1$, i.e. with a single (virtual) $\widetilde{\text{ra}}$ polynomial.

At the conclusion of these sumchecks, we are left with claims about the virtual $\widetilde{\text{ra}}$ polynomial. Since the polynomial is uncommitted, Jolt invokes a separate sumcheck that expresses an evaluation $\widetilde{\text{ra}}$ in terms of the constituent ${\widetilde{\text{ra}}}_i$ polynomials. The ${\widetilde{\text{ra}}}_i$ polynomials are, by definition, a tensor decomposition of $\widetilde{\text{ra}}$, so the "ra virtualization" sumcheck is the following:

$$\widetilde{\text{ra}}(r,r^{\prime })=\sum _{j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r^{\prime },j)\cdot \left(\prod _{i=1}^d{\widetilde{\text{ra}}}_i(r_i,j)\right)$$

Output Check

Jolt ensures correctness of guest program outputs via the output check sumcheck. Guest I/O operations, including outputs, inputs, and termination or panic bits, occur within a designated memory region. At execution completion, outputs and relevant status bits are written into this region.

Verifying that the claimed outputs and status bits are correct amounts to checking that the following polynomials agree at the indices corresponding to the program I/O memory region:

Note that val_io is only contains information known by the verifier. To check that these two polynomials are equal, we use the following sumcheck:

$$0=\sum _{k\in \{0,1{\}}^{\log K}}\widetilde{\text{eq}}(r_{\text{address}},k)\cdot \widetilde{\text{io-range}}(k)\cdot \left({\widetilde{\text{Val}}}_{\text{final}}(k)-{\widetilde{\text{Val}}}_{\text{io}}(k)\right)$$

where $\widetilde{\text{io-range}}$ is a "masking" polynomial, equal to 1 at all the indices corresponding to the program I/O region and 0 elsewhere. The MLE for a masking polynomial that isolates the range $[\text{start},\text{end})$ can be written as follows:

$${\widetilde{\text{mask}}}_{\text{start, end}}(r)=\widetilde{\text{LT}}(r,\text{end})-\widetilde{\text{LT}}(r,\text{start})$$

It is implemented in code as RangeMaskPolynomial.

This output check sumcheck generates a claim about the final memory state polynomial (${\widetilde{\text{Val}}}_{\text{final}}$), which, being virtual, is proven using the ${\widetilde{\text{Val}}}_{\text{final}}$ evaluation sumcheck:

$${\widetilde{\text{Val}}}_{\text{final}}(r)-{\widetilde{\text{Val}}}_{\text{init}}(r)=\sum _{j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{Inc}}(j)\cdot \widetilde{\text{ra}}(r,j)$$

Intuitively, the delta between the final and initial state of some memory cell is the sum of all increments to that cell.

You may have noticed in the above expression that $\widetilde{\text{Inc}}(j)$ if a polynomial only over cyclce variables, while the book describes $\widetilde{\text{Inc}}:{\mathbb{F}}^{\log K}\times {\mathbb{F}}^{\log T}\to \mathbb{F}$. This change is explained in wv virtualization.

Both the ${\widetilde{\text{Val}}}_{\text{final}}$ and $\widetilde{\text{Val}}$ evaluation sumchecks use the virtual $\widetilde{\text{ra}}$ polynomial, with claims subsequently proven via ra virtualization sumcheck.

Instruction execution

One distinguishing feature of Jolt among zkVM architectures is how it handles instruction execution, i.e. proving the correct input/output behavior of every RISC-V instruction in the trace. This is primarily achieved through the Shout lookup argument.

Large Lookup Tables and Prefix-Suffix Sumcheck

The Shout instance for instruction execution must query a massive lookup table -- effectively of size $2^{64}$, since the lookup query is constructed from two 32-bit operands. This $K>>T$ parameter regime is discussed in the Twist and Shout paper (Section 7), which proposes the use of sparse-dense sumcheck. However, upon implementation it became clear that sparse-dense sumcheck did not generalize well to the full RISC-V instruction set.

Instead, Jolt introduces a new algorithm: prefix-suffix sumcheck, described in the appendix of Proving CPU Executions in Small Space. Like the sparse-dense algorithm, it requires some structure in the lookup table:

• The lookup table must have an MLE that is efficiently evaluable by the verifier. The JoltLookupTable trait encapsulates this MLE.
• The lookup index can be split into a prefix and suffix, such that MLEs can be evaluated independently on the two parts and then recombined to obtain the desired lookup entry.
• Every prefix/suffix MLE is efficiently evaluable (constant time) on Boolean inputs

The prefix-suffix sumcheck algorithm can be conceptualized as a careful application of the distributive law to reduce the number of multiplications required for a sumcheck that would otherwise be intractably large.

To unpack this, consider the read-checking sumcheck for Shout, as presented in the paper.

$$\widetilde{\text{rv}}(r_{\text{cycle}})=\sum _{k=(k_1,\dots ,k_d)\in {\left(\{0,1{\}}^{\log (K)/d}\right)}^d,j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r_{\text{cycle}},j)\cdot \left(\prod _{i=1}^d{\widetilde{\text{ra}}}_i(k_i,j)\right)\cdot \widetilde{\text{Val}}(k)$$

Naively, this would require $\Theta (dKT)$ multiplications, which is far too large given $d=8$ and $K=2^{64}$. But suppose $\widetilde{\text{Val}}$ has prefix-suffix structure. The key intuition of prefix-suffix structure is captured by the following equation:

$$\widetilde{\text{Val}}(k_{\text{prefix}},k_{\text{suffix}})=\sum _{(\text{prefix},\text{suffix})\in \text{decompose}(\text{Val})}\widetilde{\text{prefix}}(k_{\text{prefix}})\cdot \widetilde{\text{suffix}}(k_{\text{suffix}})$$

You can think of $k_{\text{prefix}}$ and $k_{\text{suffix}}$ as the high-order and low-order "bits" of $k$, respectively, obtained by splitting $k$ at some partition index. The PrefixSuffixDecomposition trait specifies which prefix/suffix MLEs to evaluate and how to combine them.

We will split $k$ four times at four different indices, and these will induce the four phases of the prefix-suffix sumcheck. Each of the four phases encompasses 16 rounds of sumcheck (i.e. 16 of the address variables $k$), so together they comprise the first $\log K=64$ rounds of the read-checking sumcheck.

Given our prefix-suffix decomposition of $\widetilde{\text{Val}}$, we can rewrite our read-checking sumcheck as follows:

$$\widetilde{\text{rv}}(r_{\text{cycle}})=\sum _{k_{\text{prefix}}\in \{0,1{\}}^{16},k_{\text{suffix}}\in \{0,1{\}}^{48},j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r_{\text{cycle}},j)\cdot \widetilde{\text{ra}}(k_{\text{prefix}},k_{\text{suffix}},j)\cdot \sum _{(\text{prefix},\text{suffix})}\widetilde{\text{prefix}}(k_{\text{prefix}})\cdot \widetilde{\text{suffix}}(k_{\text{suffix}})$$

Note that we have replaced ${\prod }_{i=1}^d{\widetilde{\text{ra}}}_i(k_i,j)$ with just $\widetilde{\text{ra}}$. Since ${\prod }_{i=1}^d{\widetilde{\text{ra}}}_i(k_i,j)$ is degree 1 in each $k$ variable, we will treat it as a single multilinear polynomial while we're binding those variables (the first $\log K$ rounds). The equation as written above depicts the first phase, where $k_{\text{prefix}}$ is the first 16 variables of $k$, and $k_{\text{suffix}}$ is the last 48 variables of $k$.

Rearranging the terms in the sum, we have:

$$\widetilde{\text{rv}}(r_{\text{cycle}})=\sum _{k_{\text{prefix}}\in \{0,1{\}}^{16}}\sum _{(\text{prefix},\text{suffix})}\widetilde{\text{prefix}}(k_{\text{prefix}})\cdot \left(\sum _{k_{\text{suffix}}\in \{0,1{\}}^{48},j\in \{0,1{\}}^{\log T}}\widetilde{\text{ra}}(k_{\text{prefix}},k_{\text{suffix}},j)\cdot \widetilde{\text{eq}}(r_{\text{cycle}},j)\cdot \widetilde{\text{suffix}}(k_{\text{suffix}})\right)$$

Note that the summand is degree 2 in $k_{\text{prefix}}$, the variables being bound in the first phase:

1. $k_{\text{prefix}}$ appears in $\widetilde{\text{prefix}}(k_{\text{prefix}})$
2. $k_{\text{prefix}}$ also appears in appears in the paranthesized expression in $\widetilde{\text{ra}}(k_{\text{prefix}},k_{\text{suffix}},j)$

Written in this way, it becomes clear that we can treat the first 16 rounds as a mini-sumcheck over just the 16 $k_{\text{prefix}}$ variables, and with just multilinear terms. If we can efficiently compute the $2^{16}$ coefficients of each mulitlinear term, the rest of this mini-sumcheck is efficient. Each evaluation of $\widetilde{\text{prefix}}(k_{\text{prefix}})$ can be computed in constant time, so that leaves the parenthesized term:

$$\left(\sum _{k_{\text{suffix}}\in \{0,1{\}}^{48},j\in \{0,1{\}}^{\log T}}\widetilde{\text{ra}}(k_{\text{prefix}},k_{\text{suffix}},j)\cdot \widetilde{\text{eq}}(r_{\text{cycle}},j)\cdot \widetilde{\text{suffix}}(k_{\text{suffix}})\right)$$

This can be computed in $\Theta (T)$: since $\widetilde{\text{ra}}$ is one-hot, we can do a single iteration over $j\in \{0,1{\}}^{\log T}$ and only compute the terms of the sum where $\widetilde{\text{ra}}(k_{\text{prefix}},k_{\text{suffix}},j)=1$. We compute a table of $\widetilde{\text{eq}}(r_{\text{cycle}},j)$ evaluation a priori, and $\widetilde{\text{suffix}}(k_{\text{suffix}})$ can be evaluated in constant time on Boolean inputs.

After the first phase, the high-order 16 variables of $k$ will have been bound. We will need to use a new sumcheck expression for the next phase:

$$\widetilde{\text{rv}}(r_{\text{cycle}})=\sum _{k_{\text{prefix}}\in \{0,1{\}}^{16}}\sum _{(\text{prefix},\text{suffix})}\widetilde{\text{prefix}}(r^{(1)},k_{\text{prefix}})\cdot \left(\sum _{k_{\text{suffix}}\in \{0,1{\}}^{32},j\in \{0,1{\}}^{\log T}}\widetilde{\text{ra}}(r^{(1)},k_{\text{prefix}},k_{\text{suffix}},j)\cdot \widetilde{\text{eq}}(r_{\text{cycle}},j)\cdot \widetilde{\text{suffix}}(k_{\text{suffix}})\right)$$

Now $r^{(1)}\in {\mathbb{F}}^{16}$ are random values that the first 16 variables were bound to, and $k_{\text{prefix}}$ are the next 16 variables of $k$. Meanwhile, $k_{\text{suffix}}$ now represents the last 32 variables of $k$.

This complicates things slightly, but the algorithm follows the same blueprint as in phase 1. This is a sumcheck over the 16 $k_{\text{prefix}}$ variables, and there are two multilinear terms. We can still compute each evaluation of $\widetilde{\text{prefix}}(r^{(1)},k_{\text{prefix}})$ in constant time, and we can still compute the parenthesized term in $\Theta (T)$ time (observe that there is exactly one non-zero coefficient of $\widetilde{\text{ra}}(r^{(1)},k_{\text{prefix}},k_{\text{suffix}},j)$ per cycle $j$).

After the first $\log K$ rounds of sumcheck, we are left with:

$$\sum _{j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r_{\text{cycle}},j)\cdot \widetilde{\text{ra}}(r_{\text{address}},j)\cdot \widetilde{\text{Val}}(r_{\text{address}})$$

which we prove using the standard linear-time sumcheck algorithm. Note that $\widetilde{\text{ra}}(r_{\text{address}},j)$ here is a virtual polynomial.

Prefix and Suffix Implementations

Jolt modularizes prefix/suffix decomposition using two traits:

• SparseDensePrefix (under prefixes/)
• SparseDenseSuffix (under suffixes/)

Each prefix/suffix used in a lookup table implements these traits.

Multiplexing Between Instructions

An execution trace contains many different RISC-V instructions. Note that there is a many-to-one relationship between instructions and lookup tables -- multiple instructions may share a lookup table (e.g., XOR and XORI). To manage this, Jolt uses the InstructionLookupTable trait, whose lookup_table method returns an instruction's associated lookup table, if it has one (some instructions do not require a lookup).

Boolean lookup table flags indicate which table is active on a given cycle. At most one flag is set per cycle. These flags allow us to "multiplex" between all of the lookup tables:

$$\sum _{\ell }{\widetilde{\text{flag}}}_{\ell }(j)\cdot {\widetilde{\text{Val}}}_{\ell }(k)$$

where the sum is over all lookup tables $\ell$.

Only one table's flag $\textsf{flag}}_{\ell}(j)$ is 1 at any given cycle $j$, so only that table's ${\widetilde{\text{Val}}}_{\ell }(k)$ contributes to the sum.

This term becomes a drop-in replacement for $\widetilde{\text{Val}}$ as it appears in the Shout read-checking sumcheck:

$$\widetilde{\text{rv}}(r_{\text{cycle}})=\sum _{k=(k_1,\dots ,k_d)\in {\left(\{0,1{\}}^{\log (K)/d}\right)}^d,j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r_{\text{cycle}},j)\cdot \left(\prod _{i=1}^d{\widetilde{\text{ra}}}_i(k_i,j)\right)\cdot \left(\sum _{\ell }{\widetilde{\text{flag}}}_{\ell }(j)\cdot {\widetilde{\text{Val}}}_{\ell }(k)\right)$$

Note that each ${\widetilde{\text{Val}}}_{\ell }$ here has prefix-suffix structure.

raf Evaluation

The $\widetilde{\text{raf}}$-evaluation sumcheck in Jolt deviates from the description in the Twist/Shout paper. This is mostly an artifact of the prefix-suffix sumcheck, which imposes some required structure on the lookup index (i.e. the "address" variables $k$).

Case 1: Interleaved operands

Consider, for example, the lookup table for XOR x y. Intuitively, the lookup index must be crafted from the bits of x and y. A first attempt might be to simply concatenate the bits of x and y, i.e.:

$$(k_1,k_2,\dots ,k_{64})=(x_1,x_2,\dots ,x_{32},y_1,y_2,\dots ,y_{32})$$

Unfortunately, there is no apparent way for this formulation to satisfy prefix-suffix structure. Instead we will interleave the bits of x and y, i.e.

$$(k_1,k_2,\dots ,k_{64})=(x_1,y_1,x_2,y_2,\dots ,x_{32},y_{32})$$

With this formulation, the prefix-suffix structure is easily apparent. Suppose the prefix-suffix split index is 16, so:

$$\begin{gathered} k_{\text{prefix}}=(x_1,y_1,x_2,y_2,\dots ,x_8,y_8) \\ {k}_{\text{suffix}}=(x_9,y_9,x_{10},y_{10},\dots ,x_{32},y_{32}) \end{gathered}$$

Then XOR x y has the following prefix-suffix decomposition:

$$\begin{gathered} {\widetilde{\text{Val}}}_{\text{XOR}}(k_{\text{prefix}},k_{\text{suffix}})={\widetilde{\text{prefix}}}_{\text{XOR}}(k_{\text{prefix}})+{\widetilde{\text{suffix}}}_{\text{XOR}}(k_{\text{suffix}}) \\ {\widetilde{\text{prefix}}}_{\text{XOR}}(k_{\text{prefix}})=2^{31}\cdot \left(x_1+y_1-2x_1{y}_1\right)+2^{31}\cdot \left(x_2+y_2-2x_2{y}_2\right)+\cdots +2^{24}\cdot \left(x_8+y_8-2x_8{y}_8\right) \\ {\widetilde{\text{suffix}}}_{\text{XOR}}(k_{\text{prefix}})=2^{23}\cdot \left(x_9+y_9-2x_9{y}_9\right)+2^{22}\cdot \left(x_{10}+y_{10}-2x_{10}{y}_{10}\right)+\cdots +2^0\cdot \left(x_{32}+y_{32}-2x_{32}{y}_{32}\right) \end{gathered}$$

By inspection, ${\widetilde{\text{prefix}}}_{\text{XOR}}(k_{\text{prefix}})$ effectively computes the 8-bit XOR of the high-order bits of x and y, while ${\widetilde{\text{suffix}}}_{\text{XOR}}$ computes the 24-bit XOR of the low-order bits of x and y. Then the full result XOR x y is obtained by concatenating (adding) the two results.

Now that we've confirmed that we have something with prefix-suffix structure, we can write down the $\widetilde{\text{raf}}$-evaluation sumcheck expression. Instead of a single $\widetilde{\text{raf}}$ polynomial, here we have two lookup operands x and y, which are called LeftLookupOperand and RightLookupOperand in code. These are the values that appear in Jolt's R1CS constraints. The point of the $\widetilde{\text{raf}}$-evaluation sumcheck is to relate these (non-one-hot) polynomials to their one-hot counterparts. In the context of instruction execution Shout, this means the $\widetilde{\text{ra}}$ polynomial.

Since we have two $\widetilde{\text{raf}}$-like polynomials, we have two sumcheck instances:

$$\begin{gathered} \widetilde{\text{LeftLookupOperand}}(r)=\sum _{k,j}\widetilde{\text{eq}}(r,j)\cdot \widetilde{\text{ra}}(k,j)\cdot \sum _{\ell =0}^{\log (K)/2-1}{2}^{\ell }\cdot k_{2\ell } \\ \widetilde{\text{RightLookupOperand}}(r)=\sum _{k,j}\widetilde{\text{eq}}(r,j)\cdot \widetilde{\text{ra}}(k,j)\cdot \sum _{\ell =0}^{\log (K)/2-1}{2}^{\ell }\cdot k_{2\ell +1} \end{gathered}$$

This captures the interleaving behavior we described above: LeftLookupOperand is the concatenation of the "odd bits" of $k$, while RightLookupOperand is the concatenation of the "even bits" of $k$.

Case 2: Single operand

Many RISC-V instructions are similar to XOR, in that interleaving the operand bits lends itself to prefix-suffix structure. However, there are some instructions where this is not the case. The execution of some arithmetic instructions, for example, are handled by computing the corresponding operation in the field, and applying a range-check lookup to the result to truncate potential overflow bits.

In this case, the lookup index corresponds to the (single) value y being range-checked, so we do not interleave its bits with another operand. Instead, we just have:

$$(k_1,k_2,\dots ,k_{64})=(0,0,\dots ,0,y_1{y}_2,\dots ,y_{32})$$

In this case, we have the following sumchecks:

$$\begin{gathered} \widetilde{\text{LeftLookupOperand}}(r)=0 \\ \widetilde{\text{RightLookupOperand}}(r)=\sum _{k,j}\widetilde{\text{eq}}(r,j)\cdot \widetilde{\text{ra}}(k,j)\cdot \sum _{\ell =0}^{\log (K)-1}{2}^{\ell }\cdot k_{\ell } \end{gathered}$$

LeftLookupOperand is 0 and RightLookupOperand will be the concatenation of all the bits of $k$.

In order to handle Cases 1 and 2 simultaneously, we can use the same "multiplexing" technique as in the read-checking sumcheck. We use a flag polynomial to indicate which case we're in:

$$\widetilde{\text{InterleaveOperands}}(j)=1-\widetilde{\text{AddOperands}}(j)-\widetilde{\text{SubtractOperands}}(j)-\widetilde{\text{MultiplyOperands}}(j)$$

where $\widetilde{\text{AddOperands}}$, $\widetilde{\text{SubtractOperands}}$, and $\widetilde{\text{MultiplyOperands}}$ are circuit flags.

Prefix-suffix structure

These sumchecks have similar structure to the read-checking sumcheck. A side-by-side comparison of the read-checking sumcheck with the sumchecks for Case 1:

$$\begin{gathered} \widetilde{\text{rv}}(r)=\sum _{k,j}\widetilde{\text{eq}}(r,j)\cdot \widetilde{\text{ra}}(k,j)\cdot \widetilde{\text{Val}}(k) \\ \widetilde{\text{LeftLookupOperand}}(r)=\sum _{k,j}\widetilde{\text{eq}}(r,j)\cdot \widetilde{\text{ra}}(k,j)\cdot \sum _{\ell =0}^{\log (K)/2-1}{2}^{\ell }\cdot k_{2\ell } \\ \widetilde{\text{RightLookupOperand}}(r)=\sum _{k,j}\widetilde{\text{eq}}(r,j)\cdot \widetilde{\text{ra}}(k,j)\cdot \sum _{\ell =0}^{\log (K)/2-1}{2}^{\ell }\cdot k_{2\ell +1} \end{gathered}$$

As it turns out, ${\sum }_{\ell =0}^{\log (K)/2-1}{2}^{\ell }\cdot k_{2\ell }$ and ${\sum }_{\ell =0}^{\log (K)/2-1}{2}^{\ell }\cdot k_{2\ell +1}$ have prefix-suffix structure, so we can also use the prefix-suffix algorithm for these sumchecks. Due to their similarities, we batch the read-checking and these $\widetilde{\text{raf}}$-evaluation sumchecks together in a bespoke fashion.

Other sumchecks

ra virtualization

The lookup tables used for instruction execution are of size $K=2^{64}$, so we set $d=8$ as our decomposition parameter such that $K^{1/d}=2^8$.

Similar to the RAM Twist instance, we opt to virtualize the $\widetilde{\text{ra}}$ polynomial. In other words, Jolt simply carries out the read checking and $\widetilde{\text{raf}}$ evaluation sumchecks as if $d=1$.

At the conclusion of these sumchecks, we are left with claims about the virtual $\widetilde{\text{ra}}$ polynomial. Since the polynomial is uncommitted, Jolt invokes a separate sumcheck that expresses an evaluation $\widetilde{\text{ra}}$ in terms of the constituent ${\widetilde{\text{ra}}}_i$ polynomials. The ${\widetilde{\text{ra}}}_i$ polynomials are, by definition, a tensor decomposition of $\widetilde{\text{ra}}$, so the "$\widetilde{\text{ra}}$ virtualization" sumcheck is the following:

$$\widetilde{\text{ra}}(r,r^{\prime })=\sum _{j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r^{\prime },j)\cdot \left(\prod _{i=1}^d{\widetilde{\text{ra}}}_i(r_i,j)\right)$$

Since the degree of this sumcheck is $d+1=9$, using the standard linear-time sumcheck prover algorithm would make this sumcheck relatively slow. However, we employ optimizations specific to high-degree sumchecks, adapting techniques from the Karatsuba and Toom-Cook multiplication algorithms.

One-hot checks

Jolt enforces that the ${\widetilde{\text{ra}}}_i$ polynomials used for instruction execution are one-hot, using a Booleanity and Hamming weight sumcheck as described in the paper. These implementations follow the Twist and Shout paper closely, with no notable deviations.

Bytecode

At each cycle of the RISC-V virtual machine, the current instruction (as indicated by the program counter) is "fetched" from the bytecode and decoded. In Jolt, this is proven by treating the bytecode as a lookup table, and fetches as lookups. To prove the correctness of these lookups, we use the Shout lookup argument.

One distinguishing feature of the bytecode Shout instance is that we have multiple instances of the read-checking and $\widetilde{\text{raf}}$-evaluation sumchecks. Intuitively, the bytecode serves as the "ground truth" of what's being executed, so one would expect many virtual polynomial claims to eventually lead back to the bytecode. And this holds in practice –– in the Jolt sumcheck DAG diagram, we see that there are three colors of edges (corresponding to stages 1, 2, and 3,) pointing to the bytecode read-checking node, and two colors of edges (corresponding to stages 1 and 3) pointing to the bytecode $\widetilde{\text{raf}}$-evaluation node.

Each stage has its a unique opening point, so having in-edges of different colors implies that multiple instances of that sumcheck must be run in parallel to prove the different claims.

Read-checking

Another distinguishing feature of the bytecode Shout instance is that we treat each entry of lookup table as containing a tuple of values, rather than a single value. Intuitively, this is because each instruction in the bytecode encodes multiple pieces of information: opcode, operands, etc.

The figure below loosely depicts the relationship between bytecode and $\widetilde{\text{Val}}$ polynomial.

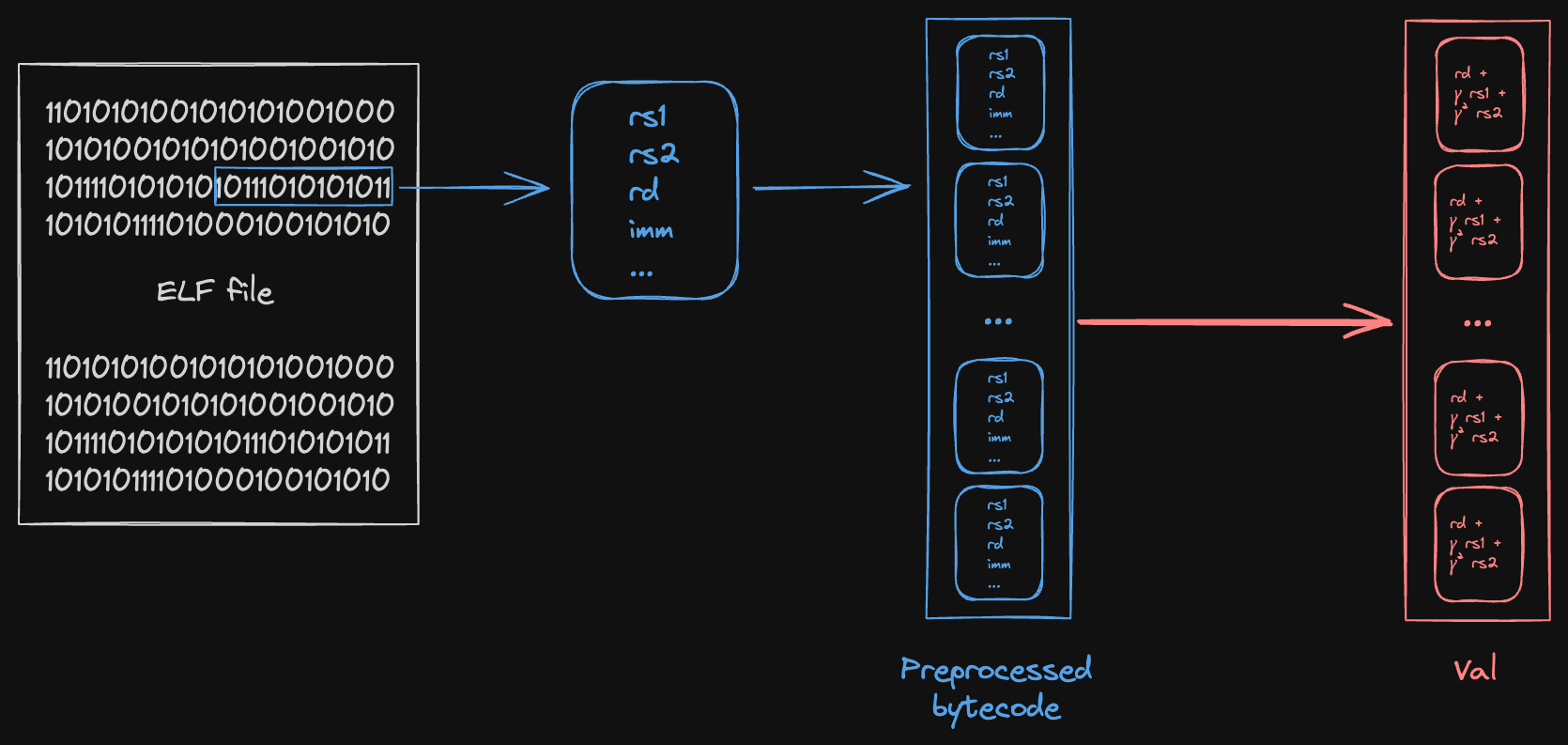
We start from some ELF file, compiled from the guest program. For each instruction in the ELF (raw bytes), we decode/preprocess the instruction into a structured format containing the individual witness values used in Jolt:

• The instruction operands rs1, rs2, rd, imm
• Circuit and lookup table flags
• The instruction address

Then, we compute a Reed-Solomon fingerprint of some subset of the values in the tuple, depending on what $\widetilde{\text{rv}}$ claims are being proven. These fingerprints serve as the coefficients of the $\widetilde{\text{Val}}$ polynomial for that read-checking instance.

The figure above depicts the $\widetilde{\text{Val}}$ polynomial we would use to prove the read-checking instance for the Stage 2 claims, labeled as "ra/wa claims" in the DAG diagram. As explained below, the $\widetilde{\text{ra}}$ and $\widetilde{\text{wa}}$ polynomials correspond to the registers (rs1, rs2, rd) in the bytecode. Each coefficient in $\widetilde{\text{Val}}$ is $\text{rd}+\gamma \cdot \text{rs1}+{\gamma }^2\cdot \text{rs2}$, for the registers of one particular instruction.

We can write the read-checking sumcheck expression for the Stage 2 claims as the following:

$${\widetilde{\text{rv}}}_{\text{rd}}(r)+\gamma \cdot {\widetilde{\text{rv}}}_{\text{rs1}}(r)+{\gamma }^2\cdot {\widetilde{\text{rv}}}_{\text{rs2}}(r)=\sum _{k,j}\widetilde{\text{eq}}(r,j)\cdot \widetilde{\text{ra}}(k,j)\cdot \left({\widetilde{\text{Val}}}_{\text{rd}}(k)+\gamma \cdot {\widetilde{\text{Val}}}_{\text{rs1}}(k)+{\gamma }^2\cdot {\widetilde{\text{Val}}}_{\text{rs2}}(k)\right)$$

where we treat

$$\widetilde{\text{Val}}(k)={\widetilde{\text{Val}}}_{\text{rd}}(k)+\gamma \cdot {\widetilde{\text{Val}}}_{\text{rs1}}(k)+{\gamma }^2\cdot {\widetilde{\text{Val}}}_{\text{rs2}}(k)$$

as a single multilinear polynomial.

Observe that this sumcheck satisfies our needs for the Stage 2 claims: ${\widetilde{\text{rv}}}_{\text{rd}}(r)$, ${\widetilde{\text{rv}}}_{\text{rs1}}(r)$, ${\widetilde{\text{rv}}}_{\text{rs2}}(r)$ are the claims output by the registers read/write-checking sumcheck, and we can simply compute Reed-Solomon fingerprint of these claims to obtain the left-hand side (i.e. input claim) of sumcheck expression above.

Registers

Technically, the explanation above glosses over some details for the sake of exposition. To be precise, the claims output by registers read/write-checking are actually:

$$\begin{gathered} {\widetilde{\text{wa}}}_{\text{rd}}(r_{\text{address}},r_{\text{cycle}}) \\ {\widetilde{\text{ra}}}_{\text{rs1}}(r_{\text{address}},r_{\text{cycle}}) \\ {\widetilde{\text{ra}}}_{\text{rs2}}(r_{\text{address}},r_{\text{cycle}}) \end{gathered}$$

where $r_{\text{address}}\in {\mathbb{F}}^{\log (\text{\# registers})}$.

So we define:

$$\widetilde{\text{Val}}(k)=\widetilde{\text{rd}}(k,r_{\text{address}})+\gamma \cdot \widetilde{\text{rs1}}(k,r_{\text{address}})+{\gamma }^2\cdot \widetilde{\text{rs2}}(k,r_{\text{address}})$$

where $\forall k\in \{0,1{\}}^{\log (\text{bytecode size})},k^{\prime }\in \{0,1{\}}^{\log (\text{\# registers})}$:

• $\widetilde{\text{rd}}(k,k^{\prime })=1$ if the $k$-th instruction in the bytecode has $rd=k^{\prime }$
• $\widetilde{\text{rd}}(k,k^{\prime })=0$ otherwise

and similarly for $\widetilde{\text{rs1}}$ and $\widetilde{\text{rs2}}$.

Equivalently,

$$\widetilde{\text{Val}}(k)=\widetilde{\text{eq}}(\text{rd}[k],r_{\text{address}})+\gamma \cdot \widetilde{\text{eq}}(\text{rs1}[k],r_{\text{address}})+{\gamma }^2\cdot \widetilde{\text{eq}}(\text{rs2}[k],r_{\text{address}})$$

where $\text{rd}[k]$ (respectively, $\text{rs1}[k]$ and $\text{rs2}[k]$) is the bitvector denoting the rd (respectively, rs1 and rs2) for the $k$-th instruction in the bytecode.

Instruction address

Each instruction in the bytecode has two associated "addresses":

• its index in the expanded bytecode. "Expanded" bytecode refers to the preprocessed bytecode, after instructions are expanded to their virtual sequences
• its memory address as given by ELF. All the instructions in a virtual sequence are assigned the address of the "real" instruction they were expanded from.

The former is used for the $\widetilde{\text{raf}}$-evaluation sumcheck, described below. The latter is used to enforce program counter updates in the [R1CS constraints] (./r1cs_constraints.md), and is treated as a part of the tuple of values in the preprocessed bytecode.

The "outer" and shift sumchecks in Spartan output claims about the virtual UnexpandedPC polynomial, which corresponds to the latter. These claims are proven using bytecode read-checking.

Flags

There are two types of Boolean flags used in Jolt:

• Circuit flags, used in R1CS constraints
• Lookup table flags, used in the instruction execution Shout

The associated flags for a given instruction in the bytecode can be computed a priori (i.e. in preprocessing), so any claims about these flags arising output by Spartan or instruction execution Shout are also proven using bytecode read-checking.

raf-evaluation

There are two $\widetilde{\text{raf}}$-evaluation instances for bytecode, corresponding to $\widetilde{\text{raf}}$ claims arising from stages 1 and 3.

The $\widetilde{\text{raf}}$ polynomial, in the context of bytecode, is the program counter (PC). The two sumchecks that output claims about the PC are the "outer" and "shift" sumchecks used to prove Jolt's R1CS constraints.

One-hot checks

Jolt enforces that the ${\widetilde{\text{ra}}}_i$ polynomials used for bytecode Shout are one-hot, using a Booleanity and Hamming weight sumcheck as described in the paper. These implementations follow the Twist and Shout paper closely, with no notable deviations.

Batched opening proof

The final stage (stage 5) of Jolt is the batched opening proof. Over the course of the preceding stages, we obtain polynomial evaluation claims that must be proven using the polynomial commitment scheme's opening proof. Instead of proving these openings "just-in-time", we accumulate them and defer the opening proof to the last stage (see ProverOpeningAccumulator and VerifierOpeningAccumulator for how this accumulation is implemented). By waiting until the end, we can batch-prove all of the openings, instead of proving them individually. This is important because the Dory opening proof is relatively expensive for the prover, so we want to avoid doing it multiple times.

Three layers of reduction

In order to reduce all of the polynomial evaluation claims into a single opening, we use the subprotocols described in Batched Openings, in a layered protocol.

Layer 1

All of the polynomials in Jolt fall into one of two categerories: one-hot polynomials (the $\widetilde{\textsf{ra}$ and $\widetilde{\textsf{wa}$ arising in Twist/Shout), and dense polynomials (we use this to mean anything that's not one-hot).

For dense polynomials evaluated at the same point, we apply the Multiple polynomials, same point subprotocol to reduce them to a single dense polynomial evaluated at that point.

We do not do the same for the one-hot polynomials, because (a) they are usually evaluated at different points, and (b) we handle them lazily in RLCPolynomial.

By doing this first layer of reduction, we reduce the number of sumcheck instances required in Layer 2:

Layer 2

Layer 2 is an instance of the Multiple polynomials, multiple points subprotocol, which is effectively just a batched sumcheck. This is the fifth and final batched sumcheck in Jolt.

Each sumcheck instance represents either:

• a dense polynomial evaluation claim (represented by DensePolynomialProverOpening), or
• a one-hot polynomial evaluation claim (represented by OneHotPolynomialProverOpening)

The batched sumcheck leaves us with evaluation claims for multiple polynomials, all evaluated at the same point, leading us to Layer 3:

Layer 3

Layer 3 is another instance of the Multiple polynomials, same point subprotocol. Unlike the usage in Layer 1, we must take a linear combination of both dense and one-hot polynomials. This is implemented in RLCPolynomial, described below.

On the verifier side, this entails taking a linear combination of commitments. Since Dory is an additively homomorphic commitment scheme, the verifier is able to do so.

Layer 3 leaves us with a single evaluation claim, which is finally proven using the Dory opening proof.

RLCPolynomial

We use the RLCPolynomial struct to represent a random linear combination (RLC) of multiple polynomials, which may include both dense and one-hot polynomials. We handle the two types separately:

• We eagerly compute the RLC of the dense polynomials. So if there are $N$ dense polynomials, each of length $T$ in the RLC, we compute the linear combination of their coefficients and store the result in the RLCPolynomial struct as a single vector of length $T$.
• We lazily compute the RLC of the one-hot polynomials. So if there are $N$ one-hot polynomials, we store $N$ (coefficient, reference) pairs in RLCPolynomial to represent the RLC. Later in the Dory opening proof when we need to compute a vector-matrix product using RLCPolynomial, we do so by computing the vector-matrix product using the individual one-hot polynomials (as well as the dense RLC) and taking the linear combination of the resulting vectors.

Twist and Shout

🚧 These docs are under construction 🚧

👷If you are urgently interested in this specific page, open a Github issue and we'll try to expedite it.👷

One-hot polynomials

Shout

Prefix-suffix Shout

Twist

"Local" vs "alternative" algorithm

wv virtualization

In the Twist and Shout paper (Figure 9), the read and write checking sumchecks of Twist are presented as follows:

Observe that the write checking sumcheck is presented as a way to confirm that an evaluation of $\widetilde{\text{Inc}}:{\mathbb{F}}^{\log K}\times {\mathbb{F}}^{\log T}\to \mathbb{F}$ is correct.

Under this formulation, both $\widetilde{\text{Inc}}$ and the $\widetilde{\text{wv}}:{\mathbb{F}}^{\log T}\to \mathbb{F}$ polynomial are committed.

With a slight tweak, we can avoid committing to $\text{wv}$. First, we will modify $\widetilde{\text{Inc}}$ to be a polynomial over just the cycle variables, i.e. $\widetilde{\text{Inc}}:{\mathbb{F}}^{\log T}\to \mathbb{F}$. Intuitively, the $j$th coefficient of $\widetilde{\text{Inc}}$ is the delta for the memory cell accessed at cycle $j$ (agnostic to which cell was accessed).

Second, we will reformulate the write checking sumcheck to more closely match the read checking sumcheck:

$$\widetilde{\text{wv}}(r^{\prime })=\sum _{k=(k_1,\dots ,k_d)\in {\left(\{0,1{\}}^{\log (K)/d}\right)}^d,j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r,k)\cdot \widetilde{\text{eq}}(r^{\prime },j)\cdot \left(\left(\prod _{i=1}^d{\widetilde{\text{wa}}}_i(k_i,j)\right)\cdot \left(\widetilde{\text{Val}}(k,j)+\widetilde{\text{Inc}}(j)\right)\right)$$

Intuitively, the write value at cycle $j$ is equal to whatever was already in that register ($\widetilde{\text{Val}}(k,j)$), plus the increment ($\widetilde{\text{Inc}}$).

We also need to tweak the $\widetilde{\text{Val}}$-evaluation sumcheck to accommodate the modification $\widetilde{\text{Inc}}$. As presented in the paper:

After modifying $\widetilde{\text{Inc}}$ to be a polynomial over just the cycle variables:

$$\widetilde{\text{Val}}(r_{\text{address}},r_{\text{cycle}})=\sum _{j^{\prime }\in \{0,1{\}}^{\log T}}\widetilde{\text{Inc}}(j^{\prime })\cdot \widetilde{\text{wa}}(r_{\text{address}},j^{\prime })\cdot \widetilde{\text{LT}}(j^{\prime },r_{\text{cycle}})$$

Dory

🚧 These docs are under construction 🚧

👷If you are urgently interested in this specific page, open a Github issue and we'll try to expedite it.👷

Optimizations

This section describes notable optimizations implemented in the Jolt codebase.

• Batched sumcheck
• Batched openings
• Inlines
• Small value optimizations
• EQ optimizations

Batched sumcheck

There is a standard technique for batching multiple sumcheck instances together to reduce verifier cost and proof size.

Consider a batch of two sumchecks:

• Sumcheck A is over $n$ variables, and has degree $j$
• Sumcheck B is over $m$ variables, and has degree $k$

If we were to prove them serially, we would have one proof of size $\Theta (nj)$ and one proof of size $\Theta (mk)$ (and the same asymptotics for verifier cost). If we instead prove them in parallel (i.e. as a batched sumcheck), we would instead have a single proof of size $\Theta (\max (n,m)\cdot \max (j,k))$.

For details, refer to Jim Posen's "Perspectives on Sumcheck batching".

Our implementation of batched sumcheck is uses the SumcheckInstance trait to represent individual instances, and the BatchedSumcheck enum to house the batch prove/verify functions.

"Bespoke" batching

In some cases, we opt to implement a "bespoke" batched sumcheck prover rather than using the BatchedSumcheck pattern. For example, the read-checking and raf-evaluation sumchecks for the instruction execution Shout instance are batched in a bespoke fashion, as are the read-checking and write-checking sumchecks in both Twist instances (RAM and registers)

The reason for doing so is prover efficiency: consider two sumchecks:

$$\begin{gathered} {\text{claim}}_1=\sum _{x}f(x)\cdot g(x)\cdot h(x) \\ {\text{claim}}_2=\sum _{x}f(x)\cdot g(x)\cdot p(x) \end{gathered}$$

The batched sumcheck expression is:

$${\text{claim}}_1+\gamma \cdot {\text{claim}}_2=\sum _{x}f(x)\cdot g(x)\cdot h(x)+\gamma \cdot f(x)\cdot g(x)\cdot p(x)$$

for some random $\gamma \in \mathbb{F}$.

Using the BatchedSumcheck trait, the prover message for each round would be computed by:

1. Computing the prover message for $f(x)\cdot g(x)\cdot h(x)$, which is some univariate polynomial $m_1(X)$.
2. Computing the prover message for $f(x)\cdot g(x)\cdot p(x)$, which is some univariate polynomial $m_2(X)$.
3. Computing the linear combination $m_1(X)+\gamma \cdot m_2(x)$.

As a general rule of thumb, the number of field multiplications required to compute the sumcheck prover message in round $i$ (using the standard linear-time sumcehck algorithm) is $(d-1)\cdot n/2^i$, where $d$ is the number of multiplications appearing in the summand expression. So with the BatchedSumcheck pattern, the prover must perform $2n/2^i$ field multiplications for both steps 1 and 2, for a total of $4n/2^i$ multiplications. If we instead leverage the shared terms in the batched sumcheck expression, we can reduce the total number of multiplications. We can rearrange the terms of the batched sumcheck expression:

$${\text{claim}}_1+\gamma \cdot {\text{claim}}_2=\sum _{x}f(x)\cdot g(x)\cdot \left(h(x)+\gamma \cdot p(x)\right)$$

By factoring out the shared $f(x)\cdot g(x)$, we can directly compute $m_1(X)+\gamma \cdot m_2(x)$ using only $3n/2^i$ multiplications.

Batched openings

Jolt uses techniques to batch multiple polynomial openings into a single opening claim to amortize the cost of Dory opening proof. There are different notions of "batched openings", each necessitating its own subprotocol.

Multiple polynomials, same point

$$f(x),g(x),\dots$$

If the polynomials are committed using an additively homomorphic commitment scheme (e.g. Dory), then this case can be reduced to a single opening claim. See Section 16.1 of Proof, Arguments, and Zero-Knowledge for details of this subprotocol.

Multiple polynomials, multiple points

$$f(x),g(y),\dots$$

The most generic case.

Consider the case of two polynomials, opened at two different points $f(r_f),g(r_g)$. We can use a batched sumcheck to reduce this to two polynomials opened at the same point. The two sumchecks in the batch are:

$$\begin{gathered} f(r_f)=\sum _x\widetilde{\text{eq}}(r_f,x)\cdot f(x) \\ g(r_g)=\sum _x\widetilde{\text{eq}}(r_g,x)\cdot g(x) \end{gathered}$$

so the batched sumcheck expression is:

$$f(r_f)+\gamma \cdot g(r_g)=\sum _x\widetilde{\text{eq}}(r_f,x)\cdot f(x)+\gamma \cdot \widetilde{\text{eq}}(r_g,x)\cdot g(x)$$

This sumcheck will produce output claims $f(r^{\prime })$ and $g(r^{\prime })$, where $r^{\prime }$ consists of the verifier (or Fiat-Shamir) challenges chosen over the course of the sumcheck.

If we further wish to reduce the claims $f(r^{\prime })$ and $g(r^{\prime })$ into a single claim, we can invoke the "Multiple polynomials, same point" subprotocol above.

This subprotocol was first described (to our knowledge) in Lemma 6.2 of Local Proofs Approaching the Witness Length [Ron-Zewi, Rothblum 2019].

One polynomial, multiple points

$$f(x),f(y),\dots$$

Though this can be considered a special case of the above, there is also a subprotocol specific for this type of batched opening: see Section 4.5.2 of Proof, Arguments, and Zero-Knowledge. We do not use this subprotocol in Jolt.

Inlines

Overview

Jolt inlines are a unique optimization technique that replaces high-level operations with optimized sequences of native RISC-V instructions. Unlike traditional precompiles that operate in a separate constraint system, inlines remain fully integrated within the main Jolt zkVM execution model, requiring no additional "glue" logic for memory correctness. Similar to the virtual sequences already used for certain RISC-V instructions, inlines expand into sequences of simpler operations, but with additional optimizations like extended registers and custom instructions.

Key Characteristics

Native RISC-V Integration: Inlines expand into sequences of RISC-V instructions that execute within the same trace as regular program code. This seamless integration eliminates the complexity of bridging between different proof systems.

Custom Instructions: Jolt enables the creation of custom instructions that can accelerate common operations. These custom instructions must have structured multilinear extension (MLE) polynomials, meaning that they can be evaluated efficiently in small space (see prefix-suffix sumcheck for details on structured MLEs). By ensuring all custom instructions maintain this property, Jolt achieves the performance benefits of specialized operations without sacrificing the simplicity of its proof system. This is the core innovation that distinguishes Jolt inlines from traditional precompiles or simple assembly optimizations - we compress complex operations into lookup-friendly instructions that remain fully verifiable within the main zkVM, eliminating the need for complex glue logic or separate constraint systems.

Extended Register Set: Inline sequences have access to 32 additional registers beyond the standard RISC-V register set. This expanded register space allows complex operations to maintain state in registers rather than memory, dramatically reducing load/store operations.

Example Usage

Jolt provides optimized inline implementations for common cryptographic operations. The SHA-256 implementation demonstrates the power of this approach. See the examples/sha2-chain directory for a complete example.

Basic Usage

#![allow(unused)]
fn main() {
use jolt_inlines_sha2::Sha256;

// Simple one-shot hashing
let input = b"Hello, Jolt!";
let hash = Sha256::digest(input);

// Incremental hashing
let mut hasher = Sha256::new();
hasher.update(b"Hello, ");
hasher.update(b"Jolt!");
let hash = hasher.finalize();
}

Chained Hashing Example

#![allow(unused)]
fn main() {
use jolt_inlines_sha2::Sha256;

#[jolt::provable]
fn sha2_chain(input: [u8; 32], num_iters: u32) -> [u8; 32] {
    let mut hash = input;
    for _ in 0..num_iters {
        hash = Sha256::digest(&hash);
    }
    hash
}
}

Direct Inline Assembly Access

For advanced use cases, you can invoke inlines directly through inline assembly. Jolt uses a structured encoding scheme for inline instructions:

• Opcode: 0x0B for Jolt core inlines, 0x2B for user-defined inlines
• funct7: Identifies the type of operation (e.g., 0x00 for SHA2)
• funct3: Identifies sub-instructions within that operation (e.g., 0x0 for SHA256, 0x1 for SHA256INIT)

#![allow(unused)]
fn main() {
unsafe {
    // SHA256 compression with existing state
    // opcode=0x0B (core inline), funct3=0x0 (SHA256), funct7=0x00 (SHA2 family)
    core::arch::asm!(
        ".insn r 0x0B, 0x0, 0x00, x0, {}, {}",
        in(reg) input_ptr,  // Pointer to 16 u32 words
        in(reg) state_ptr,  // Pointer to 8 u32 words
        options(nostack)
    );

    // SHA256 compression with initial constants
    // opcode=0x0B (core inline), funct3=0x1 (SHA256INIT), funct7=0x00 (SHA2 family)
    core::arch::asm!(
        ".insn r 0x0B, 0x1, 0x00, x0, {}, {}",
        in(reg) input_ptr,
        in(reg) state_ptr,
        options(nostack)
    );
}
}

Jolt CPU Advantages

The Jolt zkVM architecture provides several unique optimization opportunities that inlines can leverage:

1. Extended Virtual Registers

Inline sequences have access to 32 additional virtual registers beyond the standard RISC-V register set. This allows complex operations to maintain their entire working state in registers, eliminating hundreds of load/store operations that would otherwise be required. Importantly, this expanded register usage comes with virtually zero additional cost to the prover, making it an essentially "free" optimization from a proof generation perspective.

2. Custom Instructions

Jolt allows creation of custom instructions that can replace common multi-instruction patterns with a single operation. The key innovation here is that these instructions must have structured multilinear extensions (MLEs) that can be evaluated efficiently in small space (see prefix-suffix sumcheck). This is where the real performance gain comes from: by compressing operations into forms that work naturally with Jolt's lookup-based architecture, we achieve dramatic speedups without the complexity of traditional precompiles.

This is fundamentally different from traditional assembly optimization - we're not just rearranging instructions, we're creating new ones that are specifically designed to be "lookupable" within Jolt's proof system. For example, the ROTRI (rotate right immediate) instruction replaces the three-instruction sequence (x >> imm) | (x << (32-imm)) with a single cycle, while remaining fully verifiable through lookups because it maintains the structured MLE property.

Note that creating custom user-defined instructions is currently only available within the core Jolt codebase and not yet supported in external crates.

3. 32-bit Immediate Values

Unlike standard RISC-V which limits immediate values to 12 or 20 bits, inlines can use full 32-bit immediate values. This eliminates the need for multiple instructions to load large constants, reducing both cycle count and register usage.

Creating Custom Inlines

For implementing custom inlines, refer to the existing implementations in the jolt-inlines/ directory, particularly the SHA2 implementation in jolt-inlines/sha2/.

Key Requirements and Restrictions

When creating user-defined inlines, you must adhere to these critical requirements:

1. Opcode Space: Use opcode 0x2B for user-defined inlines (0x0B is reserved for Jolt core inlines)

2. Virtual Register Management:

   • All virtual registers (registers 32-63) must be zeroed out at the end of the inline sequence
   • This ensures clean state for subsequent operations

3. Register Preservation:

   • Inlines cannot modify any of the real 32 RISC-V registers, including the destination register (rd)
   • The inline must operate purely through memory operations and virtual registers

4. Instruction Encoding:

   • Use funct7 to identify your operation type (must be unique among user-defined inlines)
   • Use funct3 for sub-instruction variants within your operation

5. MLE Structure:

   • All custom instructions must have structured multilinear extensions (see prefix-suffix sumcheck)
   • Complex operations may need to be broken down into simpler instructions that maintain this property

Implementation Structure

A typical inline implementation consists of three main components:

1. SDK Module: Provides safe, high-level API for guest programs
2. Execution Module: Implements host-side execution logic for testing and verification
3. Trace Generator: Generates the optimized RISC-V instruction sequence that replaces the inline

Design Considerations

When designing your inline, consider:

• Register Allocation: Maximize use of the 32 additional virtual registers to minimize memory operations
• Custom Instructions: Identify patterns that could benefit from custom instructions (creating custom user-defined instructions is not available at this time)
• Immediate Values: Leverage 32-bit immediate values to reduce instruction count
• Memory Access Patterns: Structure your algorithm to minimize load/store operations

For concrete examples and implementation patterns, study the existing inline implementations in the Jolt codebase.

Future Directions

The inline system continues to evolve with planned enhancements:

• Extended instruction set: Additional custom instructions for common patterns
• Automated inline generation: Compiler-driven inline synthesis for hot code paths
• Larger register files: Expanding beyond 32 additional registers for complex algorithms
• Domain-specific optimizations: Specialized inlines for bigint arithmetic, elliptic curves, and other cryptographic primitives

Inlines represent a fundamental innovation in zkVM design, demonstrating that significant performance improvements are possible while maintaining the simplicity and verifiability of a RISC-V-based architecture.

Small value optimizations

🚧 These docs are under construction 🚧

👷If you are urgently interested in this specific page, open a Github issue and we'll try to expedite it.👷

EQ optimizations

🚧 These docs are under construction 🚧

👷If you are urgently interested in this specific page, open a Github issue and we'll try to expedite it.👷

Dao-Thaler optimization

Gruen's optimization

Appendix

This section includes supplementary background relevant to Jolt.

• Terminology and nomenclature
• Multilinear extensions
• Sumcheck
• Polynomial commitment schemes
• Memory checking and lookup arguments
• RISC-V
• Jolt 0.1.0
• Additional resources

Terminology and nomenclature

🚧 These docs are under construction 🚧

👷If you are urgently interested in this specific page, open a Github issue and we'll try to expedite it.👷

Multilinear Extensions

For any $v$-variate polynomial $g(x_1,...x_v)$, its multilinear extension $f(x_1,...x_v)$ is the polynomial which agrees over all $2^v$ points $x\in \{0,1{\}}^v$: $g(x_1,...x_v)=\tilde{f}(x_1,...x_v)\forall x\in \{0,1{\}}^v$. By the Schwartz-Zippel lemma, if $g$ and $f$ disagree at even a single input, then $g$ and $f$ must disagree almost everywhere.

For more precise details please read Section 3.5 of Proofs and Args ZK.

Engineering

In practice, MLE's are stored as the vector of evaluations over the $v$-variate boolean hypercube $\{0,1{\}}^v$. There are two important algorithms over multilinear extensions: single variable binding, and evaluation.

Single Variable Binding

With a single streaming pass over all $n$ evaluations we can "bind" a single variable of the $v$-variate multilinear extension to a point $r$. This is a critical sub-algorithm in sumcheck. During the binding the number of evaluation points used to represent the MLE gets reduced by a factor of 2:

• Before: $\tilde{f}(x_1,...x_v):\{0,1{\}}^v\to \mathbb{F}$
• After: $\widetilde{f^{\prime }}(x_1,...x_{v-1})=\tilde{f}(r,x_1,...x_{v-1}):\{0,1{\}}^{v-1}\to \mathbb{F}$

Assuming your MLE is represented as a 1-D vector of $2^v$ evaluations $E$ over the $v$-variate boolean hypercube $\{0,1{\}}^v$, indexed little-endian

• $E[1]=\tilde{f}(0,0,0,1)$
• $E[5]=\tilde{f}(0,1,0,1)$
• $E[8]=\tilde{f}(1,0,0,0)$

Then we can transform the vector $E\to E^{\prime }$ representing the transformation from $\tilde{f}(x_1,...x_v)\to \widetilde{f^{\prime }}(r,x_1,...x_{v-1})$ by "binding" the evaluations vector to a point $r$.

#![allow(unused)]
fn main() {
let n = 2 ** v;
let half = n / 2;
for i in 0..half {
    let low = E[i];
    let high = E[half + i];
    E[i] = low + r * (high - low);
}
}

Multi Variable Binding

Another common algorithm is to take the MLE $\tilde{f}(x_1,...x_v)$ and compute its evaluation at a single $v$-variate point outside the boolean hypercube $x\in {\mathbb{F}}^v$. This algorithm can be performed in $O(n)$ time by performing the single variable binding algorithm $\log (n)$ times. The time spent on $i$'th variable binding is $O(n/2^i)$, so the total time across all $\log n$ bindings is proportional to ${\sum }_{i=1}^{\log n}n/2^i=O(n)$.

The Sumcheck Protocol

Adapted from the Thaler13 exposition. For a detailed introduction to sumcheck see Chapter 4.1 of the textbook.

Suppose we are given a $v$-variate polynomial $g$ defined over a finite field $\mathbb{F}$. The purpose of the sumcheck protocol is to compute the sum:

$$H:=\sum _{b_1\in \{0,1\}}\sum _{b_2\in \{0,1\}}\cdots \sum _{b_v\in \{0,1\}}g(b_1,\dots ,b_v).$$

In order to execute the protocol, the verifier needs to be able to evaluate $g(r_1,\dots ,r_v)$ for a randomly chosen vector $(r_1,\dots ,r_v)\in {\mathbb{F}}^v$. Hence, from the verifier's perspective, the sumcheck protocol reduces the task of summing $g$'s evaluations over $2^v$ inputs (namely, all inputs in $\{0,1{\}}^v$) to the task of evaluating $g$ at a single input in $(r_1,\dots ,r_v)\in {\mathbb{F}}^v$.

The protocol proceeds in $v$ rounds as follows. In the first round, the prover sends a polynomial $g_1(X_1)$, and claims that

$$g_1(X_1)=\sum _{x_2,\dots ,x_v\in \{0,1{\}}^{v-1}}g(X_1,x_2,\dots ,x_v).$$

Observe that if $g_1$ is as claimed, then $H=g_1(0)+g_1(1)$. Also observe that the polynomial $g_1(X_1)$ has degree ${\text{deg}}_1(g)$, the degree of variable $x_1$ in $g$. Hence $g_1$ can be specified with ${\text{deg}}_1(g)+1$ field elements. In our implementation, $P$ will specify $g$ by sending the evaluation of $g_1$ at each point in the set $\{0,1,\dots ,{\text{deg}}_1(g)\}$. (Actually, the prover does not need to send $g_1(1)$, since the verifier can infer that $g_1(1)=H-g_1(0)$, as if this were not the case, the verifier would reject).

Then, in round $j>1$, $V$ chooses a value $r_{j-1}$ uniformly at random from $\mathbb{F}$ and sends $r_{j-1}$ to $P$. We will often refer to this step by saying that variable $j-1$ gets bound to value $r_{j-1}$. In return, the prover sends a polynomial $g_j(X_j)$, and claims that

$$g_j(X_j)=\sum _{(x_{j+1},\dots ,x_v)\in \{0,1{\}}^{v-j}}g(r_1,\dots ,r_{j-1},X_j,x_{j+1},\dots ,x_v).(1)$$

The verifier compares the two most recent polynomials by checking that $g_{j-1}(r_{j-1})=g_j(0)+g_j(1)$, and rejecting otherwise. The verifier also rejects if the degree of $g_j$ is too high: each $g_j$ should have degree ${\text{deg}}_j(g)$, the degree of variable $x_j$ in $g$.

In the final round, the prover has sent $g_v(X_v)$ which is claimed to be $g(r_1,\dots ,r_{v-1},X_v)$. $V$ now checks that $g_v(r_v)=g(r_1,\dots ,r_v)$ (recall that we assumed $V$ can evaluate $g$ at this point). If this test succeeds, and so do all previous tests, then the verifier accepts, and is convinced that $H=g_1(0)+g_1(1)$.

Polynomial Commitment Schemes

Polynomial commitment schemes (PCS) are a core cryptographic primitive in proof systems, including zkVMs. At a high level, they allow a prover to commit to a polynomial and later open that commitment (i.e. evaluate the underlying polynomial) at a point chosen by the verifier, while ensuring the binding property (the prover cannot change the polynomial after committing to it).

This mechanism is powerful because it allows succinct verification of polynomial relationships without the prover needing to reveal the entire polynomial. The verifier only learns the evaluation at chosen points.

Usage

A PCS comprises three algorithms (plus sometimes a preprocessing step): $\mathsf{Commit}$, $\mathsf{Prove}$, or $\mathsf{Verify}$. In the context of a larger proof system like Jolt, polynomial commitment schemes are typically used in some variation of the following flow:

0. Depending on the PCS, there may be a preprocessing step, where some public data is generated. This data may be needed for $\mathsf{Commit}$, $\mathsf{Prove}$, or $\mathsf{Verify}$. This preprocessing could involve a trusted setup (if not, it is called a transparent setup/PCS).
1. Prover commits to polynomial $P$, and the commitment $C:=\mathsf{Commit}(P)$ is sent to the verifier.
2. In some subsequent part of the proof system, the prover and verifier arrive at some claimed evaluation $x:=P(r)$ (typically for a random point $r\in {\mathbb{F}}^n$). For example, this claimed evaluation might be an output claim of a sumcheck.
3. The prover provides an opening proof for the evaluation, and sends the proof $\mathsf{Prove}(P,r)$ to the verifier.
4. The verifier then verifies the opening proof. If the verification $\mathsf{Verify}(C,r,x)$ succeeds, then the verifier can rest assured that $P(r)=x$ as claimed.

Role in Jolt

In Jolt, the prover commits to several witness polynomials derived from the execution trace being proven. These polynomial commitments are used extensively to tie together the various algebraic claims generated during proving. Jolt currently uses Dory as its polynomial commitment scheme. Dory provides an efficient method for committing to and opening one-hot polynomials, while supporting batch openings across many claims with relatively low overhead.

Further Reading

For a more formal and detailed introduction to polynomial commitment schemes, we recommend Section 7.3 of Justin Thaler’s Proofs, Arguments, and Zero Knowledge. That section explains how polynomial commitments integrate with interactive proof protocols such as GKR, and why they are essential for constructing succinct arguments.

Memory checking and lookup arguments

🚧 These docs are under construction 🚧

👷If you are urgently interested in this specific page, open a Github issue and we'll try to expedite it.👷

RISC-V

RISC-V is an open source instruction set architecture (ISA) based on established reduced instruction set computer (RISC) principles. Every RISC-V implementation must include the base integer ISA, with optional extensions available for additional functionality.

Jolt implements the base RISC-V instruction set, making it a RISC-V-compliant virtual machine. This means Jolt can execute and prove any code that compiles to RISC-V.

Supported Instruction Sets

Current ISA Configuration: RV32IM

Base Instruction Set

RV32I

RV32I is the base 32-bit integer instruction set. It's designed to be sufficient for a complete software toolchain while being simple and minimal. Everything else in RISC-V (multiplication, floating point, atomic operations) is built as extensions on top of this base ISA.

Key properties:

• 32-bit fixed-width instructions

• 32 integer registers (x0-x31), where x0 is hardwired to zero. Register x1/ra is reserved for return address linkage by jump-and-link instructions, x2/sp is conventionally used as stack pointer. Each register is 32 bits wide and used for both integer and memory address computations.

• 32-bit address space (byte-addressed and little-endian). Memory accesses can be to byte (8-bit), halfword (16-bit), or word (32-bit) sized values

• Basic arithmetic operations (add, subtract, shift, logical operations)

• Load/store architecture means memory can only be accessed through dedicated load and store instructions - all other instructions operate only on registers

• Simple addressing mode of base register plus 12-bit signed immediate offset. No complex memory addressing modes or memory-to-memory operations

• Conditional branches and jumps are supported

For detailed instruction formats and encoding, refer to the chapter 2 of specification

Extensions

"M" Standard Extension for Integer Multiplication and Division

Key properties:

• Multiplication operations generate 32-bit (lower) or 64-bit (full) results

• Separate signed and unsigned multiply instructions

• Hardware division with both signed and unsigned variants

• All operations work on values in integer registers

• Divide-by-zero results in a well-defined result (maximum unsigned value)

• Maintains the simple register-based architecture of RV32I

• Results always written to a single 32-bit register (for upper/lower multiplication results, two separate instructions are used)

• All instructions in this extension are encoded in the standard 32-bit RISC-V format

Core Operations:

• MUL: Multiplication, lower 32-bit result

• MULH/MULHU/MULHSU: Upper 32-bit multiplication (signed×signed, unsigned×unsigned, signed×unsigned)

• DIV/DIVU: Signed and unsigned division

• REM/REMU: Signed and unsigned remainder